Cho (O) và A là điểm nằm ngoài (O). Qua A vẽ tiếp tuyến AB, AC với (O) với B,C

Đề bài. Cho (O) và A là điểm nằm ngoài (O). Qua A vẽ tiếp tuyến AB, AC với (O) với B,C là tiếp điểm. OA cắt BC tại DA

a) Chứng minh OA là đường trung trực BC.

b) Chứng minh OD.DA = BD²

c) Vẽ đường kính BE, AE cắt (O) tại F. Gọi G là trung điểm của EF, đường thẳng OG cắt đường thẳng BC tại H. Chứng minh OD.OA = OG.OH

d) Chứng minh EH là tiếp tuyến của (O)

Trả lời

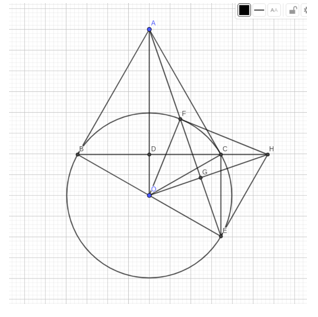a) Ta có: AB, AC là tiếp tuyến của (O) nên AB = AC

Mà OB = OC = R

Nên AO là trung trực BC

b) AB ⊥ OB, BD ⊥ OA nên OB² = OD.OA

BD² = OD.DA (hệ thức lượng trong tam giác ABO vuông tại B, BD là đường cao)

c) Xét tam giác OAG và tam giác OHD có:

Chung $\widehat{O}$

$\widehat{OGA}=\widehat{HDO}={90}^{\circ }$

⇒ ΔOAG ∼ ΔOHD (g.g)
⇒ $\frac{OA}{OH}=\frac{OG}{OD}$ hay OA.OD = OH.OG

d) Ta có: OA.OD = OH.OG = OB² = OE²

Suy ra: $\frac{OE}{OH}=\frac{OG}{OE}$

⇒ ΔOGE ∼ ΔOEH (c.g.c)

Nên: $\widehat{OEH}=\widehat{OGE}={90}^{\circ }$

Vậy EH là tiếp tuyến của (O).