Lời giải
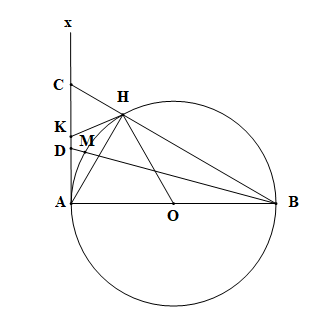
a) Vì AB là đường kính (O; R) nên AB = 2R
Vì C thuộc tiếp tuyến Ax của (O)
Nên CA ⊥ AB
Suy ra tam giác ABC vuông tại A
Vì H thuộc (O) đường kính AB
Nên tam giác ABH vuông tại H
Suy ta HA ⊥ HB
Xét tam giác ABC vuông tại A có HA ⊥ HB (chứng minh trên)
Suy ra BH . BC = AB2 = (2R)2 = 4 R2
b) Vì M thuộc (O) đường kính AB
Nên tam giác ABM vuông tại M
Suy ta MA ⊥ MB
Xét tam giác ABC vuông tại A có MA ⊥ MB (chứng minh trên)
Suy ra BM . BD = AB2
Mà BH . BC = AB2 (chứng minh câu a)
Do đó BM . BD = BH . BC
c) Vì H, A cùng thuộc (O)
Nên OA = OH
Do đó tam giác AOH cân tại O
Suy ra \(\widehat {OAH} = \widehat {OHA}\)
Vì AH ⊥ BC nên tam giác AHC vuông tại H
Suy ra \(\widehat {CAH} + \widehat {HCA} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà \(\widehat {CAH} + \widehat {HAO} = \widehat {CAO} = 90^\circ \)
Suy ra \(\widehat {OAH} = \widehat {HCA}\)
Lại có \(\widehat {OAH} = \widehat {OHA}\) (chứng minh trên)
Do đó \(\widehat {OHA} = \widehat {HCA}\) (1)
Xét tam giác AHC vuông tại H có HK là đường trung tuyến
Suy ra \(HK = KC = \frac{1}{2}AC\)
Do đó tam giác HCK cân tại K
Suy ra \(\widehat {KHC} = \widehat {KCH}\) (2)
Từ (1) và (2) suy ra \(\widehat {KHC} = \widehat {OHA}\)
Mặt khác \(\widehat {KHC} + \widehat {KHA} = \widehat {CHA} = 90^\circ \)
Suy ra \(\widehat {OHA} + \widehat {KHA} = 90^\circ \)
Hay \(\widehat {OHK} = 90^\circ \)
Nên OH ⊥ HK
Xét (O) có H thuộc (O), OH ⊥ HK
Suy ra KH là tiếp tuyến của (O)
Vậy KH là tiếp tuyến của (O).

