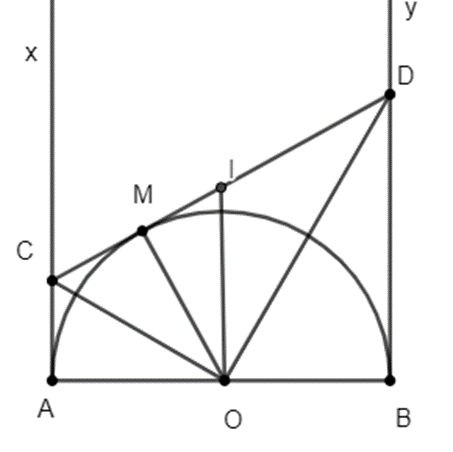
Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB.
Theo tính chất tiếp tuyến, ta có: Ax ⊥ AB; By ⊥ AB.
Suy ra: Ax // By hay AC // BD.
Suy ra tứ giác ABDC là hình thang.
Gọi I là trung điểm của CD.
Khi đó OI là đường trung bình của hình thang ABDC.
Suy ra: OI // AC ⇒ OI ⊥ AB.
Vì OC và OD lần lượt là phân giác của \(\widehat {AOM}\) và \(\widehat {BOM}\) nên:
OC\( \bot \)OD (tính chất của hai góc kề bù)
\( \Rightarrow \widehat {COD} = 90^\circ \)
Suy ra: IC = ID = IO \( = \frac{1}{2}CD\) (tính chất tam giác vuông).
Suy ra I là tâm đường tròn đường kính CD.
Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.