Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By

Đề bài: Cho nửa đường tròn tâm O có đường kính AB. Vẽ các tiếp tuyến Ax, By (Ax, By và nửa đường tròn thuộc cùng một mặt phẳng bờ AB). Gọi M là một điểm bất kì thuộc nửa đường tròn. Tiếp tuyến tại M cắt Ax, By theo thứ tự ở C và D. Chứng minh rằng đường tròn có đường kính CD tiếp xúc với AB.

Trả lời

Hướng dẫn giải:

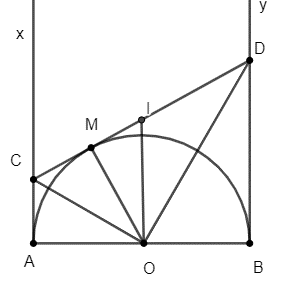
Theo tính chất tiếp tuyến, ta có: Ax ⊥ AB; By ⊥ AB.

Suy ra: Ax // By hay AC // BD.

Suy ra tứ giác ABDC là hình thang.

Gọi I là trung điểm của CD.

Khi đó OI là đường trung bình của hình thang ABDC.

Suy ra: OI // AC ⇒ OI ⊥ AB.

Vì OC và OD lần lượt là phân giác của $\widehat{AOM}$  và $\widehat{BOM}$  nên:

OC $\perp$ OD (tính chất của hai góc kề bù)

$\Rightarrow \widehat{COD}=90°$

Suy ra: IC = ID = IO $=\frac{1}{2}CD$  (tính chất tam giác vuông).

Suy ra I là tâm đường tròn đường kính CD.

Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.

Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.