Cho nửa đường tròn tâm O có đường kính AB, Ax là tiếp tuyến của nửa đường tròn

Đề bài: Cho nửa đường tròn tâm O có đường kính AB, Ax là tiếp tuyến của nửa đường tròn (Ax và nửa đường tròn nằm cùng phía đối với AB), C là một điểm thuộc nửa đường tròn, H là hình chiếu của C trên AB. Đường thẳng qua O và vuông góc với AC cắt Ax tại M. Gọi I là giao điểm của MB và CH. Chứng minh rằng CI = IH.

Trả lời

Hướng dẫn giải:

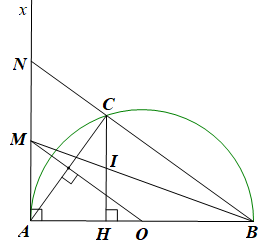
• Gọi N là giao điểm của BC và Ax.

Vì C thuộc đường tròn tâm O đường kính AB nên OA = OB = OC

Do đó DABC vuông tại C nên AC ⊥ BC.

Mà OM ⊥ AC (giả thiết) nên OM // BC hay OM // BN.

Xét DABN có OM // BN và O là trung điểm của AB

Do đó M là trung điểm của AN hay AM = MN.

• Do Ax là tiếp tuyến của (O) nên Ax ⊥ AB

Ta có: CH ⊥ AB, Ax ⊥ AB nên CH // AB.

Xét DABM có IH // AM, theo hệ quả định lí Thalès ta có: $\frac{IH}{AM}=\frac{BI}{BM}$ .

Xét DMBN có CI // MN, theo hệ quả định lí Thalès ta có: $\frac{CI}{MN}=\frac{BI}{BM}$ .

Do đó $\frac{IH}{AM}=\frac{CI}{MN}\left(=\frac{BI}{BM}\right)$

Mà AM = MN (chứng minh trên) nên IH = CI.

Vậy CI = IH.