Lời giải
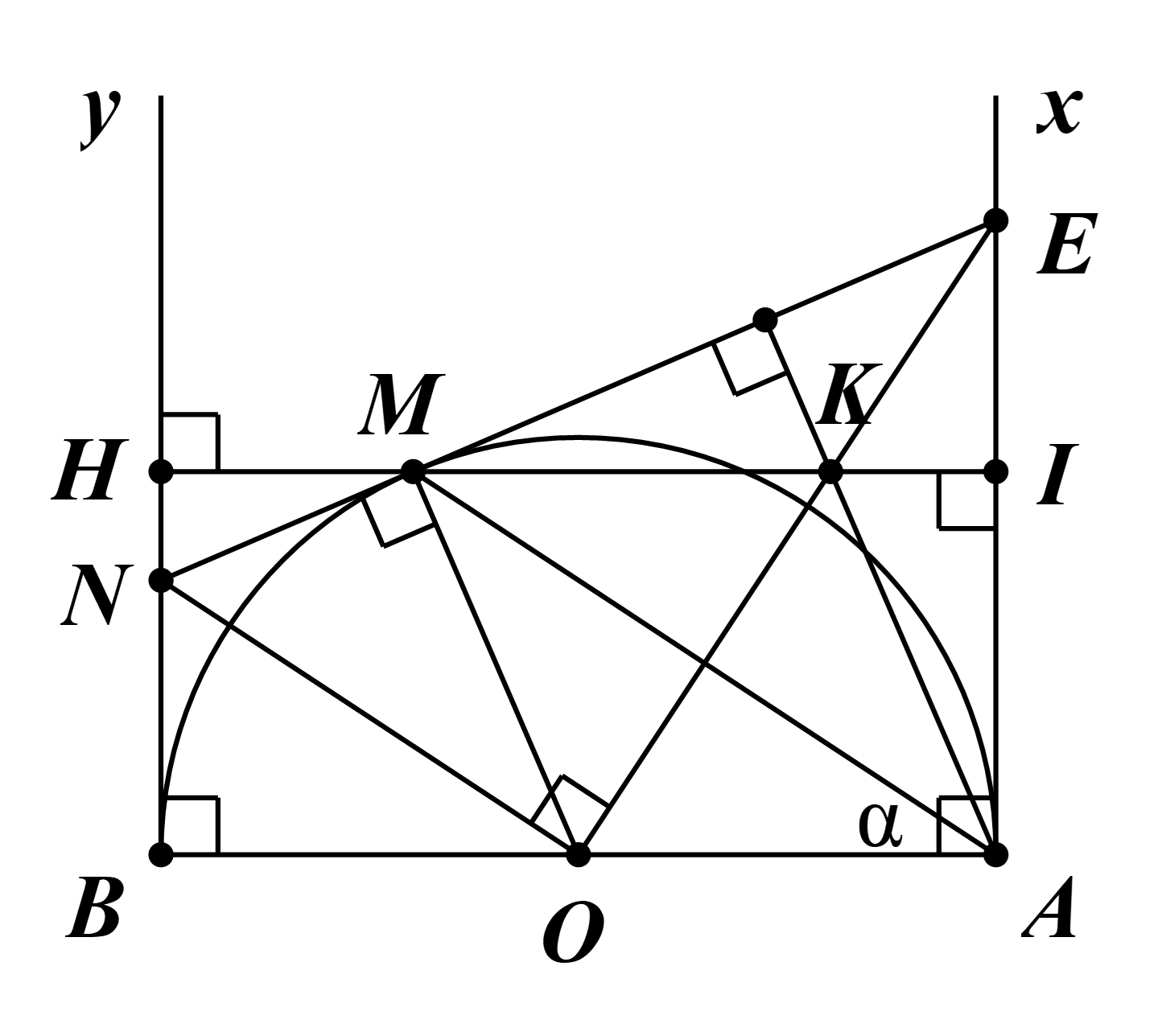
a) Ta có \(\widehat {OAE} = 90^\circ \) (AE là tiếp tuyến của nửa đường tròn (O)).
Suy ra ba điểm O, A, E cùng thuộc một đường tròn đường kính OE (1)
Ta có \(\widehat {OME} = 90^\circ \) (ME là tiếp tuyến của nửa đường tròn (O)).
Suy ra ba điểm O, M, E cùng thuộc một đường tròn đường kính OE (2)
Từ (1), (2), ta được tứ giác AOME nội tiếp đường tròn đường kính OE.
Chứng minh tương tự, ta được tứ giác BOMN nội tiếp đường tròn đường kính ON.
b) Ta có AE, ME là hai tiếp tuyến của đường tròn (O) và AE cắt ME tại E.
Suy ra AE = ME (theo tính chất hai tiếp tuyến cắt nhau).
Chứng minh tương tự, ta được MN = BN.
Ta có AE, ME là hai tiếp tuyến của đường tròn (O) và AE cắt ME tại E.
Suy ra OE là tia phân giác của \(\widehat {AOM}\) hay \(\widehat {AOE} = \widehat {EOM}\).
Chứng minh tương tự, ta được \(\widehat {BON} = \widehat {MON}\).
Đường tròn (O) có AB là đường kính.
Suy ra \(\widehat {AOB} = 180^\circ \).
Khi đó \(\widehat {AOE} + \widehat {EOM} + \widehat {MON} + \widehat {NOB} = 180^\circ \).
Vì vậy \(2\widehat {EOM} + 2\widehat {MON} = 180^\circ \).
Suy ra \(2\left( {\widehat {EOM} + \widehat {MON}} \right) = 180^\circ \).
Do đó \(\widehat {EON} = 90^\circ \).
∆EON vuông tại O có OM là đường cao.
Áp dụng hệ thức lượng trong tam giác vuông, ta có ME.MN = OM2.
Vậy AE.BN = R2.
c) Ta có By ⊥ AB (By là tiếp tuyến của (O)) và Ax ⊥ AB (Ax là tiếp tuyến của (O)).
Suy ra By // Ax.
Mà MH ⊥ By (giả thiết).
Do đó MH ⊥ Ax hay MK ⊥ AE.
∆OMA cân tại O (do OM = OA = R) có OE là đường phân giác.
Suy ra OE cũng là đường cao của ∆OMA hay EK ⊥ AM.
∆AME có MK, EK là hai đường cao cắt nhau tại K.
Suy ra K là trực tâm của ∆AME.
Vậy AK ⊥ ME hay AK ⊥ MN.
d) Ta có \(\widehat {MAB}\) là góc nội tiếp chắn và \(\widehat {MOB}\) là góc ở tâm chắn .
Suy ra \(\widehat {MOB} = 2\widehat {MAB} = 2\alpha \) và \(\widehat {BON} = \widehat {MON} = \frac{{\widehat {MOB}}}{2} = \alpha \).
Diện tích hình quạt tròn BOM là: \({S_1} = \frac{{\pi {R^2}.2\alpha }}{{360^\circ }}\).
Gọi I là giao điểm của MK và AE.
Xét ∆MNH và ∆MEI, có:
\(\widehat {HMN} = \widehat {EMI}\) (cặp góc đối đỉnh);
\(\widehat {MHN} = \widehat {MIE} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{MN}}{{ME}} = \frac{{MH}}{{MI}} = \frac{{NH}}{{EI}}\)
Khi đó \(\frac{{MN}}{{MH}} = \frac{{ME}}{{MI}} = \frac{{NH}}{{EI}}\)
Vì vậy \(\frac{{MN}}{{MH}}\,\,\left( { = \frac{{EI}}{{MI}}} \right) = \frac{{NH}}{{ME}}\)
Suy ra MN.ME = MH.NH = R2 (kết quả câu b).
Khi đó \({S_{\Delta MNH}} = \frac{1}{2}MH.HN = \frac{1}{2}{R^2}\).
Ta có OM = OB = R và BN = MN (chứng minh trên).
Suy ra OM.MN = OB.BN.
Do đó \({S_{\Delta MNO}} = {S_{\Delta BNO}}\).
Vì vậy \({S_{BOMN}} = 2{S_{\Delta MNO}} = 2.\frac{1}{2}MN.OM = O{M^2}.\tan \alpha = {R^2}.\tan \alpha \).
Vậy diện tích phần tứ giác BOMH ở bên ngoài nửa đường tròn (O) là: \(S = {S_{MNH}} + {S_{BOMN}} - {S_1} = \frac{1}{2}{R^2} + {R^2}.\tan \alpha - \frac{{\pi {R^2}.2\alpha }}{{360^\circ }} = {R^2}\left( {\frac{1}{2} + \tan \alpha - \frac{{2\pi \alpha }}{{360^\circ }}} \right)\).
e) Ta có AK ⊥ ME (kết quả câu c) và OM ⊥ ME (ME là tiếp tuyến của (O)).
Suy ra AK // OM.
Mà MK // OA (chứng minh trên).
Do đó tứ giác OAKM là hình bình hành.
Mà OE là tia phân giác của \(\widehat {AOM}\) (chứng minh trên).
Suy ra tứ giác OAKM là hình thoi.
Do đó MK = OM = R.
Vì vậy ∆OMK cân tại M.
Mà OK = R (do K nằm trên (O)).
Suy ra ∆OMK đều.
Khi đó \(\widehat {MOK} = 60^\circ \).
Vì vậy \[\widehat {AOM} = 2\widehat {MOK} = 2.60^\circ = 120^\circ \].
Vậy M nằm trên nửa đường tròn (O) sao cho \(\widehat {AOM} = 120^\circ \) thì K nằm trên đường tròn (O).

