Lời giải
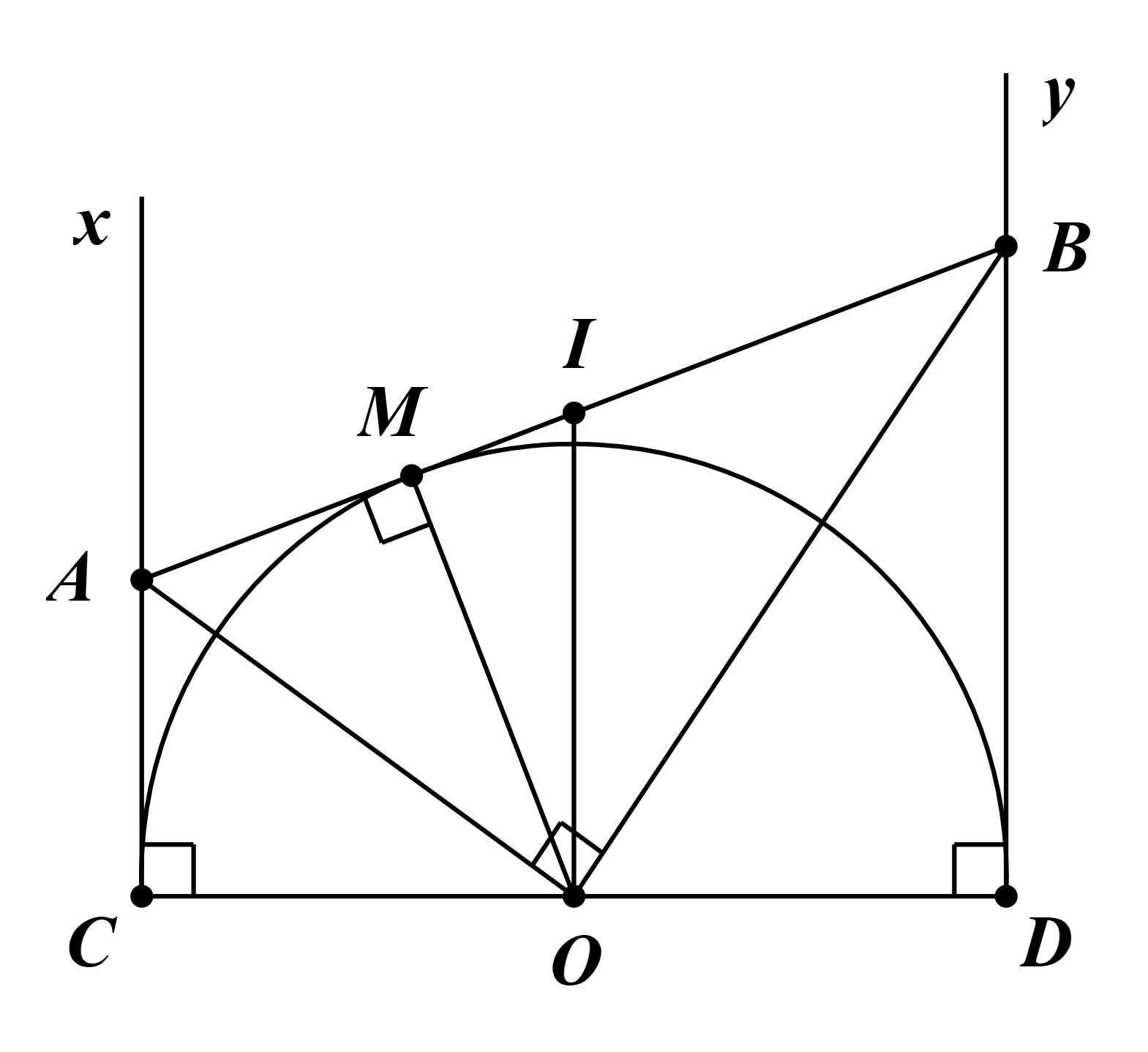
a) Vì AM, AC là hai tiếp tuyến của (O) nên ta có OA là tia phân giác của \(\widehat {COM}\).
Chứng minh tương tự, ta được OB là tia phân giác của \(\widehat {MOD}\).
Ta có \(\widehat {COM} + \widehat {MOD} = 180^\circ \) (hai góc kề bù).
\( \Leftrightarrow 2\widehat {AOM} + 2\widehat {MOB} = 180^\circ \)
\( \Leftrightarrow 2\left( {\widehat {AOM} + \widehat {MOB}} \right) = 180^\circ \)
\( \Leftrightarrow \widehat {AOM} + \widehat {MOB} = \frac{{180^\circ }}{2}\)
\( \Leftrightarrow \widehat {AOB} = 90^\circ \).
Vậy tam giác AOB vuông tại O.
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có AC = AM và BM = BD.
Ta có AB = AM + MB = AC + BD.
Vậy ta có điều phải chứng minh.
c) Gọi I là trung điểm của AB.
Suy ra I là tâm của đường tròn đường kính AB.
Ta có \(\widehat {AOB} = 90^\circ \) (chứng minh trên).
Suy ra O nằm trên đường tròn đường kính AB.
Ta có CA ⊥ CD và BD ⊥ CD (AC, BD là tiếp tuyến của đường tròn (O)).
Suy ra CA // BD.
Do đó ABDC là hình thang.
Hình thang ABDC có O, I lần lượt là trung điểm của CD và AB.
Suy ra OI là đường trung bình của hình thang ABDC.
Do đó OI // AC.
Mà AC ⊥ CD (chứng minh trên).
Suy ra OI ⊥ CD.
Vậy CD là tiếp tuyến của đường tròn đường kính AB.

