Lời giải
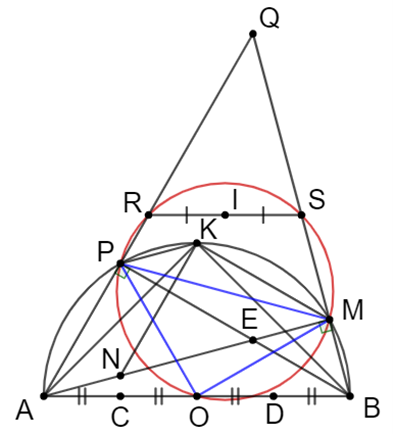
a) Xét đường tròn tâm O, đường kính AB có:
\(\widehat {APB} = \widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Nên \(\widehat {QPB} = 90^\circ ;\;\widehat {QMA} = 90^\circ \) (hai góc kề bù với hai góc trên).
Suy ra \(\widehat {QPE} + \widehat {QME} = 90^\circ + 90^\circ = 180^\circ \).
Do đó, tứ giác PQME nội tiếp đường tròn.
b) K là điểm chính giữa cung AB nên
Þ AK = KB (liên hệ giữa cung và dây)
Xét ∆AKN và ∆BKM có:
AK = BK (cmt)
\(\widehat {NAK} = \widehat {MBK}\) (Hai góc nội tiếp cùng chắn cung KM)
AN = BM (gt)
Þ ∆AKN = ∆BKM (c.g.c).
c) Xét ∆AMQ và ∆BME có:
\(\widehat {AMQ} = \widehat {BME} = 90^\circ \)
\(\widehat {QAM} = \widehat {EBM}\) (Hai góc nội tiếp cùng chắn cung MP)
Þ ∆AMQ ᔕ ∆BME (g.g)
\( \Rightarrow \frac{{AM}}{{BM}} = \frac{{AQ}}{{BE}} \Rightarrow AM.BE = BM.AQ\)
Mà AN = BM Þ AM.BE = AN.AQ
d) \(\widehat {ABM} = \widehat {RPM}\) (ABMP nội tiếp)
\(\widehat {RPM} = \widehat {QSR}\) (RPMS nội tiếp)
\( \Rightarrow \widehat {ABM} = \widehat {QSR}\) (Hai góc ở vị trí đồng vị)
Þ RS // AB
BP // KM Þ cung KP = cung MB
Þ
\( \Rightarrow \widehat {MOP} = \widehat {KOB} = 90^\circ \) (Hai góc ở tâm chắn hai cung bằng nhau)
Þ ∆OMP nội tiếp đường tròn đường kính PM
PQME nội tiếp đường tròn nên suy ra
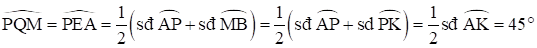
Kẻ IC // AQ, ID // BQ \( \Rightarrow \widehat {CID} = \widehat {PQM} = 45^\circ \)
RS = OM = OA = OB = R (không đổi)
Þ C, D là trung điểm của OA, OB Þ C, D cố định
I luôn nhìn CD cố định dưới góc 45°
Þ I nằm trên cung chứa góc 45° vẽ trên đoạn CD cố định.

