Cho nửa đường tròn (O) đường kính AB = 2R, N là điểm trên nửa đường tròn. Trên cùng một nửa mặt phẳng bờ AB, vẽ hai tiếp tuyến Ax và By và một tiếp tuyến tại N cắt hai tiếp tuyến Ax và By lần
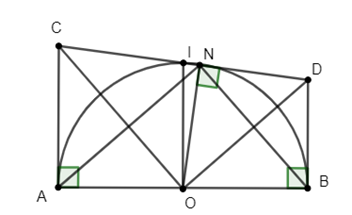
Cho nửa đường tròn (O) đường kính AB = 2R, N là điểm trên nửa đường tròn. Trên cùng một nửa mặt phẳng bờ AB, vẽ hai tiếp tuyến Ax và By và một tiếp tuyến tại N cắt hai tiếp tuyến Ax và By lần lượt tại C và D.
Chứng minh: AC + BD = CD và AC.BD không đổi.