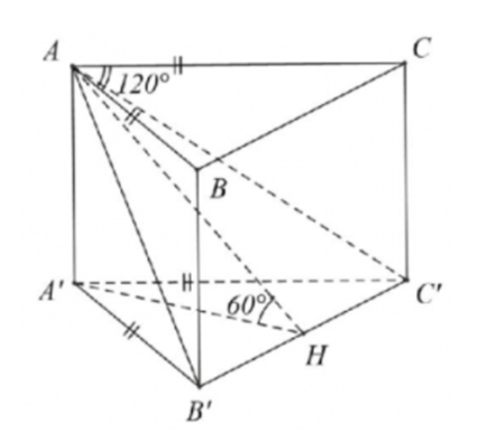
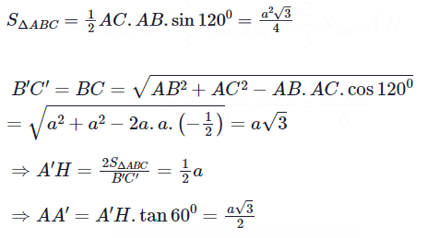Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác cân với AB = AC = a, \(\widehat {BAC} = 120^\circ \). Mặt phẳng (AB’C’) tạo với đáy một góc 60°. Tính thể tích V của khối lăng trụ đã cho

A. \(\frac{{3{{\rm{a}}^3}}}{8}\);

B. \(\frac{{{\rm{9}}{{\rm{a}}^3}}}{8}\);

C. \(\frac{{{{\rm{a}}^3}}}{8}\);

D. \(\frac{{{\rm{3}}{{\rm{a}}^3}}}{4}\).

Đáp án đúng là: A

Gọi H là trung điểm của B’C’

Khi đó góc giữa mặt phẳng (AB’C’) và đáy là góc \(\widehat {AHA'} = 60^\circ \)

Ta có:

Thể tích V của khối lăng trụ đã cho là \(V = {S_{ACB}}{\rm{.AA' = }}\frac{{{a^2}\sqrt 3 }}{4}.\frac{{a\sqrt 3 }}{2} = \frac{{3{{\rm{a}}^3}}}{8}\).

Vậy ta chọn đáp án A.