Cho khối chóp S.ABCD có đáy ABCD là hình thang cân với đáy AD và BC. Biết AD = 2a, AB = BC = CD = a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) là điểm H thuộc đoạn AD thỏa mãn HD = 3HA

Trả lời

Lời giải :

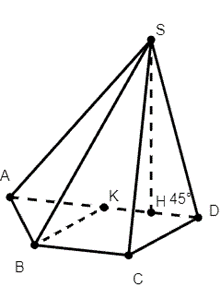
Gọi M là trung điểm của AD.

Ta có BC = AM = a và BC // AM nên tứ giác ABCM là hình bình hành.

Suy ra CM = AB = a suy ra ∆CDM đều.

Gọi K là hình chiếu của C lên AD.

Ta có: \(CK = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}}  = \frac{{a\sqrt 3 }}{2}\).

Diện tích hình thang ABCD là : \(S = \frac{{\left( {a + 2a} \right).\frac{{a\sqrt 3 }}{2}}}{2} = \frac{{3{a^2}\sqrt 3 }}{4}\).

Lại có: \(HD = \frac{3}{2}.2a = \frac{{3a}}{2}\).

Vậy thể tích của khối chóp S.ABCD là :

\(V = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}.\frac{{3a}}{2}.\frac{{3{a^2}\sqrt 3 }}{4} = \frac{{3{a^3}\sqrt 3 }}{8}\) (đvtt).

Vậy thể tích của khối chóp S.ABCD là \(\frac{{3{a^3}\sqrt 3 }}{8}\) đvtt.