Cho hình vuông ABCD cạnh a, tâm O và M là trung điểm AB. Tính độ dài của các vectơ \[\overrightarrow {OA} + \overrightarrow {OB} \,.\]
Lời giải
Ta có: \(\left| {\overrightarrow {AB} } \right| = AB = a\);
\(\left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \);
\(\left| {\overrightarrow {OA} } \right| = OA = OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\);
\(\left| {\overrightarrow {OM} } \right| = OM = \frac{{AD}}{2} = \frac{a}{2}\).
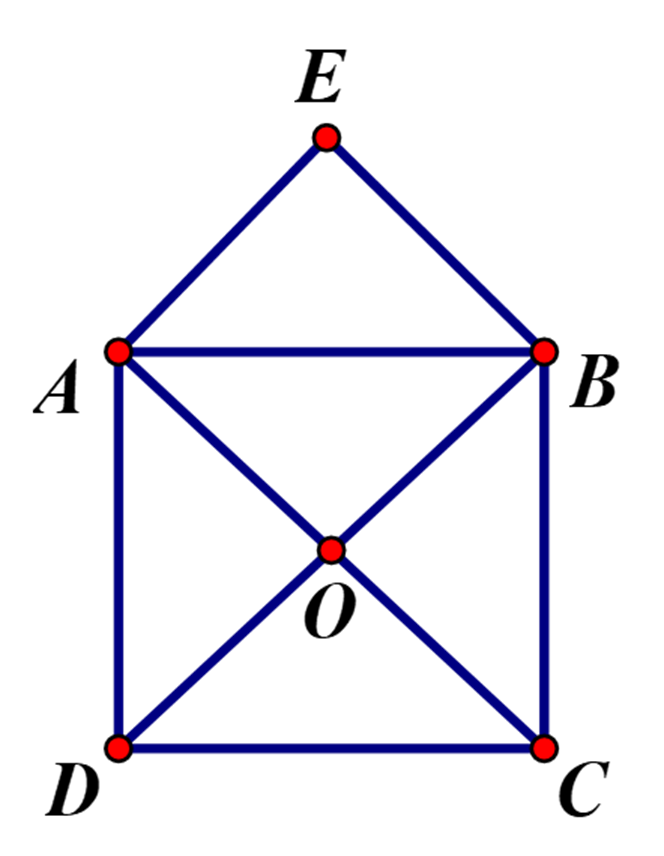
Gọi E là điểm sao cho tứ giác OBEA là hình bình hành khi đó nó cũng là hình vuông
Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OE} \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {\overrightarrow {OE} } \right| = OE = AB = a\).