Cho hình vuông ABCD tâm O cạnh a. Gọi M là trung điểm AB. Tính độ dài vecto AB , vecto AC, vecto OA, vecto OM, vecto OA  + vecto OB

Trả lời

Lời giải

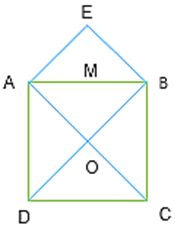
+) Vì ABCD là hình vuông nên \(\left| {\overrightarrow {AB} } \right| = AB = a\)

+) \(\left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)

+) Vì O là tâm hình vuông nên \(\left| {\overrightarrow {OA} } \right| = OA = OC = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\).

+) Vì M là trung điểm của AB nên OM là đường trung bình ∆ABD nên ta có:

\(\left| {\overrightarrow {OM} } \right| = OM = \frac{{AD}}{2} = \frac{a}{2}\).

+) \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {OE} = 2\overrightarrow {OM} \) (dựng AOBE là hình bình hành)

\( \Rightarrow \left| {\overrightarrow {OA} + \overrightarrow {OB} } \right| = \left| {2\overrightarrow {OM} } \right| = 2OM = a\).