Cho hình vuông ABCD, qua điểm M thuộc đường chéo AC kẻ ME vuông góc

Đề bài: Cho hình vuông ABCD, qua điểm M thuộc đường chéo AC kẻ ME vuông góc với AD, MF vuông góc với CD. Chứng minh rằng:

a) BE vuông góc với AF.

b) BM vuông góc với EF.

c) Các đường thẳng BM, AF và CE đồng quy.

Trả lời

Hướng dẫn giải:

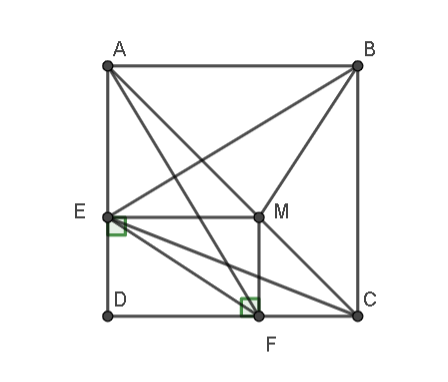
a)

Gọi giao của BM với EF là I, FM và AB là K

Vì tam giác ADF bằng tam giác BAE (cạnh huyền–cạnh góc vuông)

Nên $\widehat{DAF}=\widehat{ABE}$

⇒ $\widehat{ABE}+\widehat{BAF}=\widehat{DAF}+\widehat{BAF}$

$\Rightarrow \widehat{ABE}+\widehat{BAF}=90°$

Do đó, AF vuông góc với EB

b)

Vì ABCD là hình vuông nên AC là phân giác của $\widehat{BAD}$

Xét tứ giác AKME có

AK // ME

MK //AE

AM là phân giác của $\widehat{KAE}$

$\widehat{KAE}=90°$

Do đó, AKME là hình vuông

⇒ MK = ME và KB = MF

Do đó, tam giác KMB bằng tam giác MEF

$\Rightarrow \widehat{MFE}=\widehat{KBM}$

Mà $\widehat{KMB}=\widehat{IMF}$

$\Rightarrow \widehat{MFE}+\widehat{IMF}=\widehat{KBM}+\widehat{KMB}=90°$

Do đó, BM vuông góc với EF

c)

Xét tam giác BEF có:

BM,AF là các đường cao

nên BM cắt AF tại trực tâm của tam giác

Do đó, M là trực tâm

Vậy BM,AF,CE đồng quy