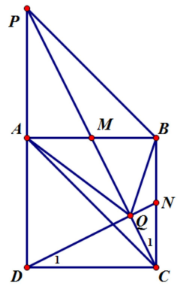
Cho hình vuông ABCD, M là trung điểm cạnh AB, P là giao điểm CM và DA

Đề bài: Cho hình vuông ABCD, M là trung điểm cạnh AB, P là giao điểm CM và DA

a) Cm: APBC là hình bình hành và BCDP là hình thang vuông

b) CM: 2Sbcdp = 3Sapbc

c) Gọi N là trung điểm BC, Q là giao điểm DN và CM. Cm: AQ = AB

Trả lời

Hướng dẫn giải:

a) Ta có: $\widehat{{\text{M}}_{\text{1}}}\text{ = }\widehat{{\text{M}}_{\text{2}}}$ (2 góc đổi đỉnh)

$\Rightarrow \text{ΔAMP = ΔBMC(g . c . g)}\Rightarrow \text{MP = MC}$

Xét tứ giác APBC có AB và CP là 2 đường chéo nhau tại trung điểm mỗi đường nên APBC là hình bình hành.
Vì APBC là hình bình hành nên $\text{BC // AP}\Rightarrow \text{BC // DP}$  mà $\text{BC }\perp \text{CD}$

$\Rightarrow$ BCDP là hình thang vuông (Điều phải chứng minh).
b) Nhận xét: ${\text{S}}_{\text{ADC}}{\text{ = S}}_{\text{ABC}}{\text{ = S}}_{\text{ABP}}$  và đặt ${\text{S}}_{\text{ADC}}{\text{ = S}}_{\text{ABC}}{\text{ = S}}_{\text{ABP}}\text{ = a}$

Khi đó: ${\text{2S}}_{\text{BCDP}}{\text{ = 2 . 3a = 6a; 3S}}_{\text{APBC}}\text{ = 3 . 2a = 6a}$

Suy ra đpcm.

c) Vì M là trung điểm của AB nên $\text{BM = }\frac{\text{1}}{\text{2}}\text{AB}$

Vì N là trung điểm của BC nên $\text{CN = }\frac{\text{1}}{\text{2}}\text{BC}$ mà

$\text{AB = BC}\Rightarrow \text{BM = CN}\Rightarrow \text{ΔCBM = ΔDCN(c . g . c)}\Rightarrow \widehat{{\text{C}}_{\text{1}}}\text{ = }\widehat{{\text{D}}_{\text{1}}}$

mà $\Delta DCN$ vuông tại C nên

$\widehat{{\text{D}}_{\text{1}}}\text{ + }\widehat{{\text{N}}_{\text{1}}}{\text{ = 90}}^{\text{o}}\Rightarrow \widehat{{\text{C}}_{\text{1}}}\text{ + }\widehat{{\text{N}}_{\text{1}}}{\text{ = 90}}^{\text{o}}\Rightarrow \widehat{\text{CQN}}{\text{ = 90}}^{\text{o}}$

$\Rightarrow \Delta PDQ$ vuông tại Q.
Xét vuông tại Q, có QA là đường trung tuyến ứng với cạnh huyền

$\Rightarrow \text{QA = }\frac{\text{1}}{\text{2}}\text{PD = AD}$  mà $\text{AD = AB}\Rightarrow \text{AQ = AB}$  (Điều phải chứng minh).