Cho hình vuông ABCD . Gọi M, N lần lượt là trung điểm BC, CD. Chứng
Cho hình vuông ABCD . Gọi M, N lần lượt là trung điểm BC, CD. Chứng minh AN ⊥ DM.
Cho hình vuông ABCD . Gọi M, N lần lượt là trung điểm BC, CD. Chứng minh AN ⊥ DM.
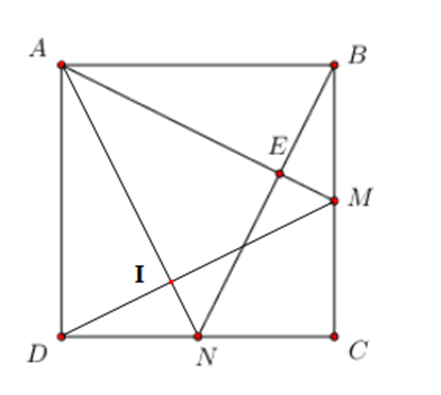
Vì ABCD là hình vuông nên AB = BC = CD = DA
Vì M, N lần lượt là trung điểm BC, CD mà DC = BC
Suy ra MC = ND
Xét ΔDMC và ΔAND có
DC = AD (chứng minh trên)
\(\widehat D = \widehat C\left( { = 90^\circ } \right)\)
MC = ND (chứng minh trên)
Suy ra ΔDMC = ΔAND (c.g.c)
Do đó \(\widehat {M{\rm{D}}C} = \widehat {NA{\rm{D}}}\) (hai góc tương ứng)
Ta có
\(\widehat {M{\rm{D}}C} + \widehat {A{\rm{DM}}} = \widehat {A{\rm{D}}C} = 90^\circ \)
Mà \(\widehat {M{\rm{D}}C} = \widehat {NA{\rm{D}}}\)
Suy ra \(\widehat {NA{\rm{D}}} + \widehat {A{\rm{DM}}} = 90^\circ \)
Gọi I là giao điểm của AN và DM
Xét tam giác ADI có
\(\widehat {NA{\rm{D}}} + \widehat {A{\rm{DM}}} + \widehat {AID} = 180^\circ \)
Suy ra \(90^\circ + \widehat {AID} = 180^\circ \)
Hay \(\widehat {AID} = 90^\circ \)
Do đó AN ⊥ DM
Vậy AN ⊥ DM .