Cho hình vuông ABCD. Gọi E là điểm đối xứng với A qua D

Đề bài: Cho hình vuông ABCD. Gọi E là điểm đối xứng với A qua D.

a) Tam giác ACE vuông cân.

b) Kẻ AH vuông góc với BE. Gọi M, N theo thứ tự là trung điểm của AH và HE. Chứng minh tứ giác BMNC là hình bình hành.

c) Chứng minh M là trực tâm của tam giác ANB.

Trả lời

Hướng dẫn giải:

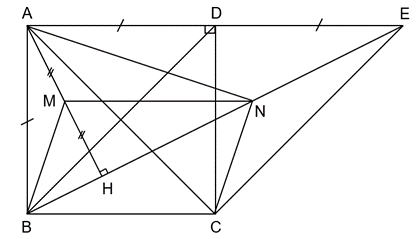
a) Ta có ABCD là hình vuông nên AB = BC = DC = AD và AC = BD (tính chất các cạnh và đường chéo của hình vuông).

Mà E đối xứng với A qua D nên DE = AD (gt)

⇒ DC = AD = DE.

⇒ ACE là tam giác vuông.

Mặc khác BC =AD = DE và BC // DE.

⇒ Tứ giác DECB là hình bình hành có BD = CE.

Mà BD = AC nền AC = CE

⇒ ACE là tam giác vuông cân.

b) Theo đề ta có:  MA = MH , NH = NE

⇒ MN là đường trung bình của ∆AHE

⇒ MN //AE và $MN=\frac{1}{2}AE$ (1)

Ta có: AD = DE (gt) nên $AD=\frac{1}{2}AE$

Vì ABCD là hình vuông nên AD = BC và AD vuông góc với AB;

nên $BC=\frac{1}{2}AE$ và DE // BC (2)

Từ (1) và (2) ⇒ MN = BC và MN//BC

⇒ Tứ giác BMNC là hình bình hành .

c) Vì BMNC là hình bình hành (câu b) nên NM // BC

ABCD là hình vuông nên CB vuông góc AB

⇒ NM ⊥ AB (đl)

Xét Δ ANB có:

AH ⊥ BN (gt)

NM ⊥ AB(cmt)

AH ∩ NM tại M

⇒ M là trực tâm của ΔANB.