Cho hình vuông ABCD có cạnh bằng a. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. M là giao điểm của CE và DF.
a) Chứng minh tứ giác EFGH là hình vuông.
b) Chứng minh DF ⊥ CE và ∆MAD cân.
c) Tính diện tích tam giác MDC theo a.
Lời giải
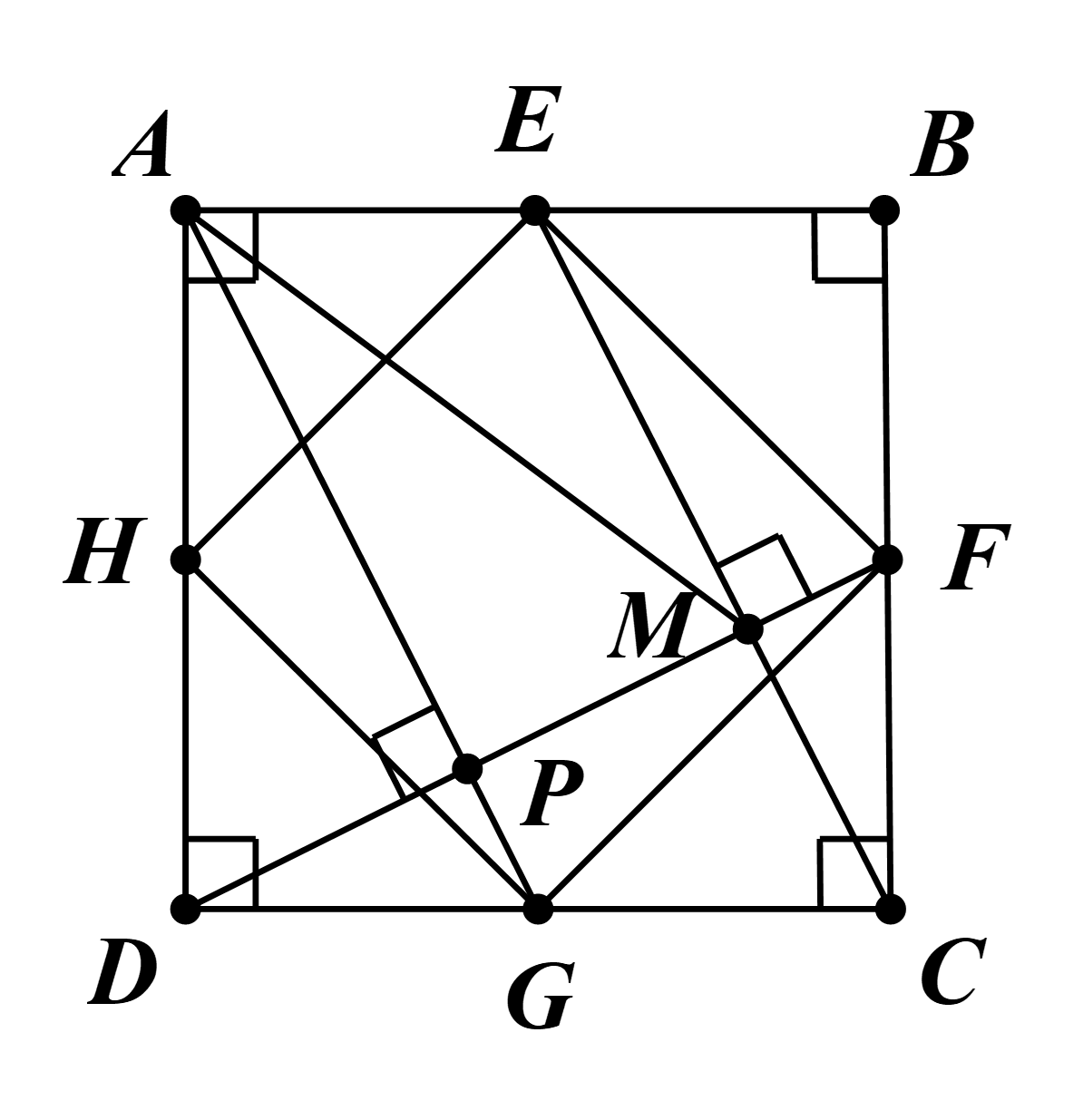
a) Xét ∆AEH và ∆BEF, có:
AE = BE (E là trung điểm AB);
AH = BF (do \(AH = \frac{1}{2}AD,\,BF = \frac{1}{2}BC\) và AD = BC);
\(\widehat {HAE} = \widehat {EBF} = 90^\circ \).
Do đó ∆AEH = ∆BEF (c.g.c).
Suy ra HE = EF (cặp cạnh tương ứng).
Chứng minh tương tự, ta được EF = GF và GH = GF.
Do đó tứ giác EFGH là hình thoi (1)
Ta có BE = BF (do \(BE = \frac{1}{2}AB,\,BF = \frac{1}{2}BC\) và AB = BC) và \(\widehat {EBF} = 90^\circ \) (do ABCD là hình vuông).
Suy ra ∆BEF vuông cân tại B.
Do đó \(\widehat {BEF} = 45^\circ \).
Chứng minh tương tự, ta được \(\widehat {AEH} = 45^\circ \).
Ta có \(\widehat {AEH} + \widehat {HEF} + \widehat {FEB} = 180^\circ \) (kề bù).
\( \Leftrightarrow \widehat {HEF} = 180^\circ - \widehat {AEH} - \widehat {FEB} = 180^\circ - 45^\circ - 45^\circ = 90^\circ \) (2)
Từ (1), (2), suy ra tứ giác EFGH là hình vuông.
b) Xét ∆CBE và ∆DCF, có:
CB = DC (ABCD là hình vuông);
\(\widehat {CBE} = \widehat {DCF} = 90^\circ \);
BE = CF (do \(BE = \frac{1}{2}AB,\,CF = \frac{1}{2}BC\) và AB = BC).
Do đó ∆CBE = ∆DCF (c.g.c).
Suy ra \(\widehat {ECB} = \widehat {FDC}\) (cặp cạnh tương ứng).
Mà \(\widehat {DFC} + \widehat {FDC} = 90^\circ \) (∆DFC vuông tại C).
Do đó \(\widehat {DFC} + \widehat {ECB} = 90^\circ \).
Tam giác CFM, có: \(\widehat {CMF} = 180^\circ - \left( {\widehat {DFC} + \widehat {ECB}} \right) = 180^\circ - 90^\circ = 90^\circ \).
Vậy DF ⊥ CE tại M.
Gọi P là giao điểm của AG và DF.
Chứng minh tương tự như trên, ta được AG ⊥ DF tại P.
Mà CE ⊥ DF (chứng minh trên).
Suy ra CE // AG.
∆DMC có: G là trung điểm của DC (giả thiết) và PG // MC (chứng minh trên).
Suy ra GP là đường trung bình của ∆DMC.
Do đó P là trung điểm DM.
∆AMD có: AP vừa là đường trung tuyến, vừa là đường cao.
Vậy ∆AMD cân tại A.
c) Xét ∆DMC và ∆DCF, có:
\(\widehat {MDC}\) chung;
\(\widehat {DMC} = \widehat {DCF} = 90^\circ \).
Do đó (g.g).
Suy ra \(\frac{{DM}}{{DC}} = \frac{{MC}}{{CF}} = \frac{{DC}}{{DF}}\) (*)
Ta có \({S_{DMC}} = \frac{1}{2}MC.MD\) và \({S_{DCF}} = \frac{1}{2}DC.CF\).
Suy ra \(\frac{{{S_{DMC}}}}{{{S_{DCF}}}} = \frac{{MC.MD}}{{DC.CF}} = \frac{{D{M^2}}}{{D{C^2}}}\).
Do đó \({S_{DMC}} = \frac{{D{M^2}}}{{D{C^2}}}.{S_{DCF}} = \frac{{D{M^2}}}{{D{C^2}}}.\frac{1}{2}CD.CF = \frac{{D{M^2}}}{{{a^2}}}.\frac{1}{2}a.\frac{a}{2} = \frac{{D{M^2}}}{4}\).
Tam giác CDF vuông tại C:
\(DF = \sqrt {D{C^2} + C{F^2}} = \sqrt {D{C^2} + {{\left( {\frac{{BC}}{2}} \right)}^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\).
Từ (*), ta có: DM.DF = DC2.
\( \Leftrightarrow DM.\frac{{a\sqrt 5 }}{2} = {a^2}\).
\( \Rightarrow DM = \frac{{2a\sqrt 5 }}{5}\).
Vậy \({S_{DMC}} = \frac{{D{M^2}}}{4} = {\left( {\frac{{2a\sqrt 5 }}{5}} \right)^2}.\frac{1}{4} = \frac{{{a^2}}}{5}\).