Cho hình vuông ABCD cạnh a. Tính độ dài vectơ vec u = 4 vecto MA - 3 vecto MB + vecto MC - 2 vecto MD.
39
14/05/2024
Cho hình vuông ABCD cạnh a. Tính độ dài vectơ \(\vec u = 4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} \).
A. \(\left| {\vec u} \right| = a\sqrt 5 \);
B. \(\left| {\vec u} \right| = \frac{{a\sqrt 5 }}{2}\);
C. \(\left| {\vec u} \right| = 3a\sqrt 5 \);
D. \(\left| {\vec u} \right| = 2a\sqrt 5 \).
Trả lời
Lời giải
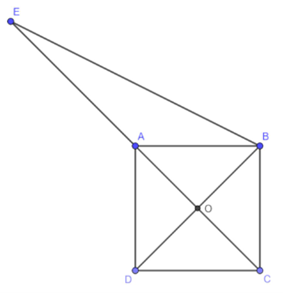
Gọi O là giao điểm của AC và BD.
⇒ O là trung điểm của AC và BD.
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OC} = \vec 0;\,\overrightarrow {OB} + \overrightarrow {OD} = \vec 0\).
Ta có \(\vec u = 4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} \)
\( = 4\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) - 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right) - 2\left( {\overrightarrow {MO} + \overrightarrow {OD} } \right)\)
\( = 3\overrightarrow {OA} + \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) - \overrightarrow {OB} - 2\left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\)
\( = 3\overrightarrow {OA} + \vec 0 - \overrightarrow {OB} - 2.\vec 0\)
\( = 3\overrightarrow {OA} - \overrightarrow {OB} \).
Lấy điểm E sao cho \(\overrightarrow {OE} = 3\overrightarrow {OA} \).
Khi đó \(\vec u = \overrightarrow {OE} - \overrightarrow {OB} = \overrightarrow {BE} \).
∆ABD vuông tại A: \(BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \).
\(AO = BO = \frac{{BD}}{2} = \frac{{a\sqrt 2 }}{2}\).
Suy ra \(OE = 3OA = \frac{{3a\sqrt 2 }}{2}\).
∆ EBO vuông tại O: \(EB = \sqrt {O{B^2} + O{E^2}} = \sqrt {{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\frac{{3a\sqrt 2 }}{2}} \right)}^2}} = a\sqrt 5 \).
Vậy \(\left| {\vec u} \right| = a\sqrt 5 \).
Do đó ta chọn phương án A.

