Cho hình vuông ABCD cạnh a. Tính độ dài vectơ AB  + vecto AC

Trả lời

Lời giải

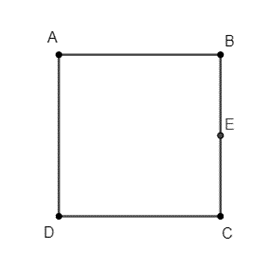
Gọi E là trung điểm của BC ta có:

\(\overrightarrow {AB} + \overrightarrow {AC} = \left( {\overrightarrow {AE} + \overrightarrow {EB} } \right) + \left( {\overrightarrow {AE} + \overrightarrow {EC} } \right)\)

\( = 2.\overrightarrow {AE} + \overrightarrow {EB} + \overrightarrow {EC} = 2\overrightarrow {AE} + \overrightarrow 0 = 2\overrightarrow {AE} \)

Mặt khác ta có: \(\left| {\overrightarrow {AE} } \right| = AE = \frac{{\sqrt 5 a}}{2}\)

Do đó \(2\left| {\overrightarrow {AE} } \right| = a\sqrt 5 \).

Vậy \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 5 \).