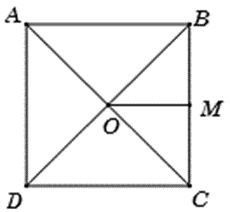
Cho hình vuông ABCD cạnh a, tâm O. Tính vecto |OB + vecto OC|. A. | vecto OB + vecto OC| = a; B. | vecto OB + vecto OC| = a căn bậc hai của 2 ; C. | vecto OB + vecto OC| = a/2
Cho hình vuông ABCD cạnh a, tâm O. Tính \[\left| {\overrightarrow {OB} + \overrightarrow {OC} } \right|.\]
A. \[\left| {\overrightarrow {OB} + \overrightarrow {OC} } \right| = a;\]
B. \[\left| {\overrightarrow {OB} + \overrightarrow {OC} } \right| = a\sqrt 2 ;\]
C. \[\left| {\overrightarrow {OB} + \overrightarrow {OC} } \right| = \frac{a}{2};\]
D. \[\left| {\overrightarrow {OB} + \overrightarrow {OC} } \right| = \frac{{a\sqrt 2 }}{2}.\]