Lời giải
a) \(2\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} = \left( {\overrightarrow {MA} - \overrightarrow {MB} } \right) + \left( {\overrightarrow {MA} - \overrightarrow {MC} } \right)\)
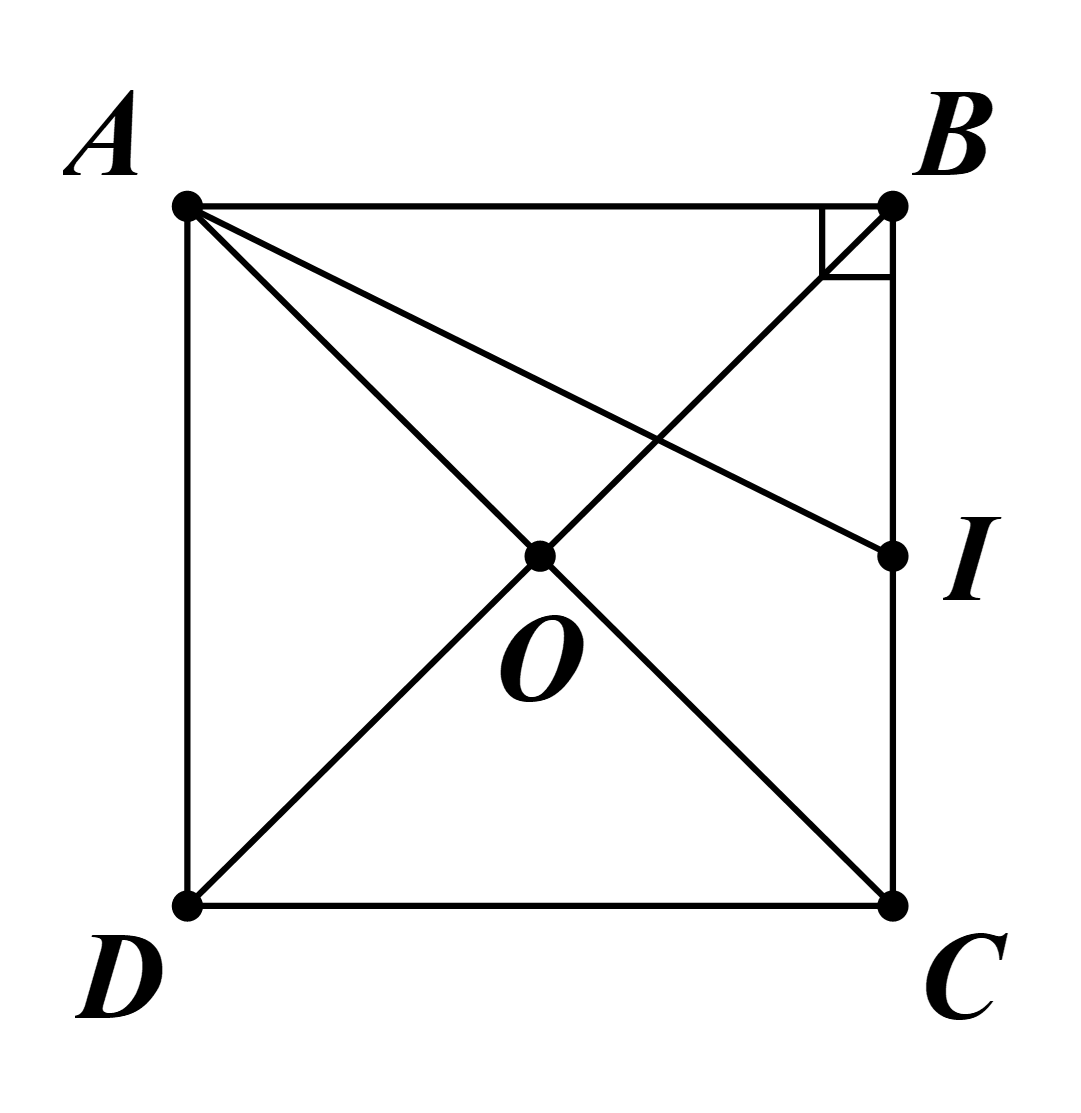
\( = \overrightarrow {BA} + \overrightarrow {CA} = - \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = - 2\overrightarrow {AI} \), với I là trung điểm BC.
Tam giác ABI vuông tại B: \(AI = \sqrt {A{B^2} + B{I^2}} = \sqrt {A{B^2} + {{\left( {\frac{{BC}}{2}} \right)}^2}} = \sqrt {{a^2} + {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 5 }}{2}\).
Ta có \(\left| {2\overrightarrow {MA} - \overrightarrow {MB} - \overrightarrow {MC} } \right| = \left| { - 2\overrightarrow {AI} } \right| = 2AI = 2.\frac{{a\sqrt 5 }}{2} = a\sqrt 5 \).
b) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} - 3\overrightarrow {MD} = \overrightarrow {MA} - \overrightarrow {MD} + \overrightarrow {MB} - \overrightarrow {MD} + \overrightarrow {MC} - \overrightarrow {MD} \)
\( = \overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DB} = 2\overrightarrow {DO} + \overrightarrow {DB} \), với O là tâm hình vuông ABCD.
\[ = \overrightarrow {DB} + \overrightarrow {DB} = 2\overrightarrow {DB} \].
Tam giác ABD vuông tại A: \(DB = \sqrt {A{B^2} + A{D^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \).
Ta có \[\left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} - 3\overrightarrow {MD} } \right| = \left| {2\overrightarrow {DB} } \right| = 2DB = 2a\sqrt 2 \].
c) \(4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} = 3\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MA} - \overrightarrow {MD} + \overrightarrow {MC} - \overrightarrow {MD} \)
\( = 3\overrightarrow {BA} + \overrightarrow {DA} + \overrightarrow {DC} = 3\overrightarrow {BA} + \overrightarrow {DA} - \overrightarrow {BA} = 2\overrightarrow {BA} + \overrightarrow {DA} \)
\( = \overrightarrow {BA} + \overrightarrow {BA} + \overrightarrow {CB} = \overrightarrow {BA} + \overrightarrow {CA} = - \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = - 2\overrightarrow {AI} \).
Ta có \(\left| {4\overrightarrow {MA} - 3\overrightarrow {MB} + \overrightarrow {MC} - 2\overrightarrow {MD} } \right| = \left| { - 2\overrightarrow {AI} } \right| = 2AI = a\sqrt 5 \).

