Câu hỏi:
01/02/2024 45Cho hình vẽ
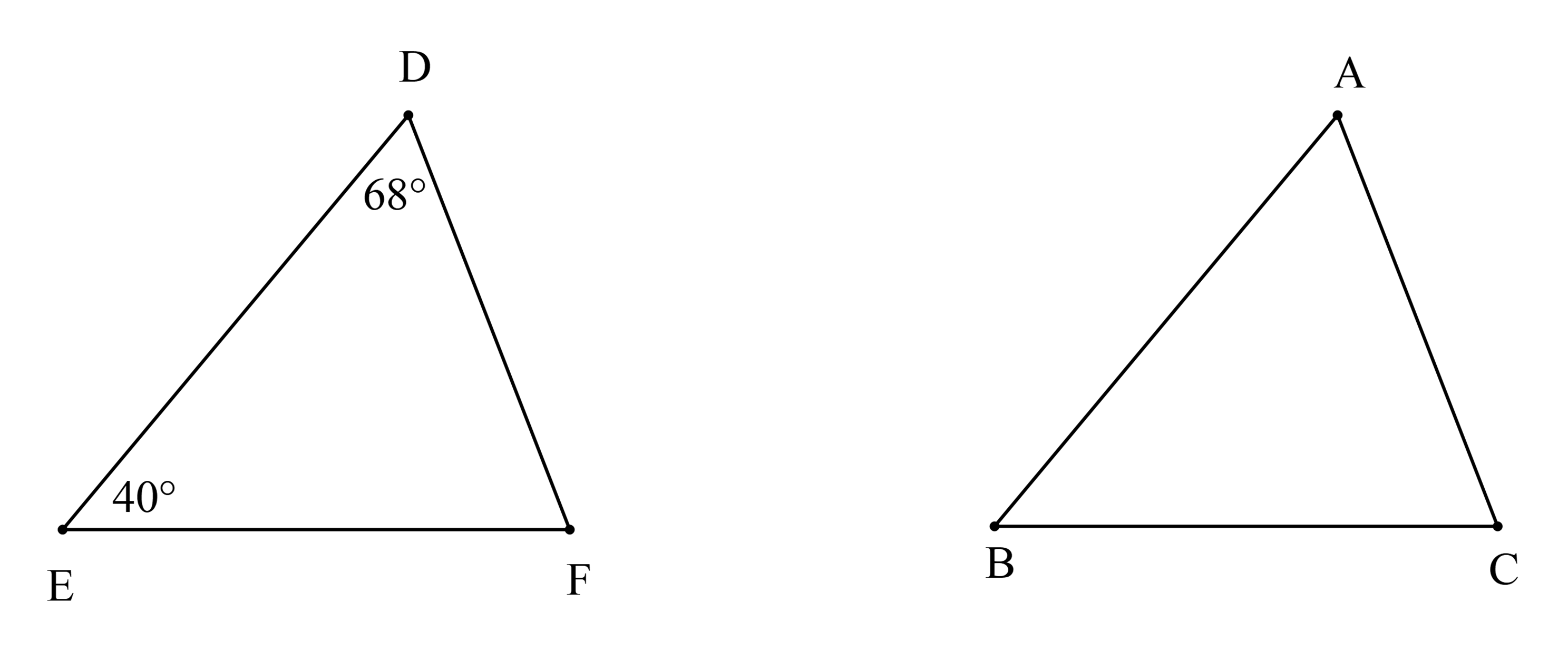
Biết ∆DEF = ∆ABC và \(\widehat {\rm{D}} = 68^\circ \); \(\widehat {\rm{E}} = 40^\circ \). Số đo của \(\widehat {\rm{C}}\) là:
A. 40°;
B. 68°;
C. 72°;
D. 82°.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆DEF có \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(68^\circ + 40^\circ + \widehat {\rm{F}} = 180^\circ \)
Suy ra \(\widehat {\rm{F}} = 180^\circ - 68^\circ - 40^\circ = 72^\circ \)
Theo bài ta có ∆DEF = ∆ABC
Suy ra \(\widehat {\rm{F}} = \widehat {\rm{C}} = 72^\circ \) (hai góc tương ứng).
Vậy ta chọn phương án C.
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆DEF có \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(68^\circ + 40^\circ + \widehat {\rm{F}} = 180^\circ \)
Suy ra \(\widehat {\rm{F}} = 180^\circ - 68^\circ - 40^\circ = 72^\circ \)
Theo bài ta có ∆DEF = ∆ABC
Suy ra \(\widehat {\rm{F}} = \widehat {\rm{C}} = 72^\circ \) (hai góc tương ứng).
Vậy ta chọn phương án C.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC vuông tại B (AB < AC) có AM là tia phân giác góc A (M ∈ BC). Trên cạnh AC lấy điểm N sao cho AB = AN. Góc bằng với \(\widehat {{\rm{BAC}}}\) là
Câu 3:
Cho tam giác ABC có AB = AC và AH là đường cao kẻ từ A. Biết \(\widehat B = 43^\circ ,\) số đo của \(\widehat {BAC}\) là