Câu hỏi:
02/02/2024 139
Cho ∆ABC cân tại A có ˆA=45∘.
Đường trung trực của cạnh AC cắt AB tại D. Trên cạnh AC lấy điểm E sao cho CE = BD. Chứng minh ∆BCD = ∆CBE. Từ đó suy ra ^BDC=^CEB.
Cho ∆ABC cân tại A có ˆA=45∘.
Đường trung trực của cạnh AC cắt AB tại D. Trên cạnh AC lấy điểm E sao cho CE = BD. Chứng minh ∆BCD = ∆CBE. Từ đó suy ra ^BDC=^CEB.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
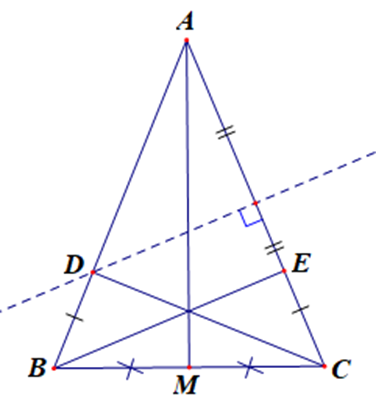
Xét ∆BCD và ∆CBE, có:
BC là cạnh chung.
CE = BD (giả thiết).
^DBC=^ECB (do ∆ABC cân tại A).
Do đó ∆BCD = ∆CBE (c.g.c)
Suy ra ^BDC=^CEB (hai góc tương ứng).

Xét ∆BCD và ∆CBE, có:
BC là cạnh chung.
CE = BD (giả thiết).
^DBC=^ECB (do ∆ABC cân tại A).
Do đó ∆BCD = ∆CBE (c.g.c)
Suy ra ^BDC=^CEB (hai góc tương ứng).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
Câu 2:
Cho ∆ABC cân tại A có ˆA=45∘.
Tính số đo các góc của tam giác ABC từ đó so sánh các cạnh của tam giác ABC.
Cho ∆ABC cân tại A có ˆA=45∘.
Tính số đo các góc của tam giác ABC từ đó so sánh các cạnh của tam giác ABC.
Câu 3:
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
Trong các biến cố trên, hãy chỉ ra biến cố nào là biến cố chắc chắn, biến cố nào là biến cố không thể.
Gieo ngẫu nhiên xúc xắc 6 mặt cân đối một lần. Xét các biến cố sau:
A: “Số chấm xuất hiện trên con xúc xắc là số lẻ và chia hết cho 3”.
B: “Số chấm xuất hiện trên con xúc xắc là số có một chữ số”.
C: “Số chấm xuất hiện trên con xúc xắc là số tròn trăm”.
D: “Số chấm xuất hiện trên con xúc xắc là số chia cho 4 dư 1”.
Trong các biến cố trên, hãy chỉ ra biến cố nào là biến cố chắc chắn, biến cố nào là biến cố không thể.Câu 4:
Cho ∆ABC cân tại A có ˆA=45∘.
Kẻ đường trung tuyến AM của tam giác ABC. Chứng minh ba đường thẳng AM, BE, CD đồng quy tại một điểm.
Cho ∆ABC cân tại A có ˆA=45∘.
Kẻ đường trung tuyến AM của tam giác ABC. Chứng minh ba đường thẳng AM, BE, CD đồng quy tại một điểm.
Câu 5:
Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8. Tính số đo mỗi góc của tam giác đó.
Số đo ba góc của một tam giác tỉ lệ với 4; 6; 8. Tính số đo mỗi góc của tam giác đó.
Câu 6:
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Tìm nghiệm của đa thức M(x) biết M(x) = P(x) + Q(x).
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Câu 7:
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Thu gọn và sắp xếp hai đa thức trên theo lũy thừa giảm dần của biến.
Câu 8:
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Tìm bậc và hệ số tự do của đa thức K(x) biết K(x) = P(x) – Q(x).
Cho hai đa thức P(x) = 6x5 + 15 – 7x – 4x2 – x5;
Q(x) = –5x5 – 2x + 4x2 + 5x – 7.
Câu 9:
Chọn câu đúng. Với điều kiện các tỉ số đều có nghĩa thì từ xy=uv ta có
Chọn câu đúng. Với điều kiện các tỉ số đều có nghĩa thì từ xy=uv ta có
Câu 10:
Tìm số nguyên x để đa thức A(x) = 2x3 – 3x2 + 2x + 2 chia hết cho đa thức B(x) = x2 + 1.
Tìm số nguyên x để đa thức A(x) = 2x3 – 3x2 + 2x + 2 chia hết cho đa thức B(x) = x2 + 1.
Câu 12:
Cho tam giác ABC với hai đường trung tuyến BM và CN cắt nhau tại G. Kết luận nào sau đây là sai?
Cho tam giác ABC với hai đường trung tuyến BM và CN cắt nhau tại G. Kết luận nào sau đây là sai?
Câu 13:
Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 = 7 và x2 = – 4; y2 = 3, giá trị của x1; y1 là
Giả sử x và y là hai đại lượng tỉ lệ thuận, x1; x2 là hai giá trị khác nhau của x và y1; y2 là hai giá trị tương ứng của y. Biết y1 – x1 = 7 và x2 = – 4; y2 = 3, giá trị của x1; y1 là


