Trắc nghiệm Toán 7 CTST Bài 2. Tam giác bằng nhau có đáp án (Phần 2) (Thông hiểu)
-
223 lượt thi
-
7 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho hình vẽ
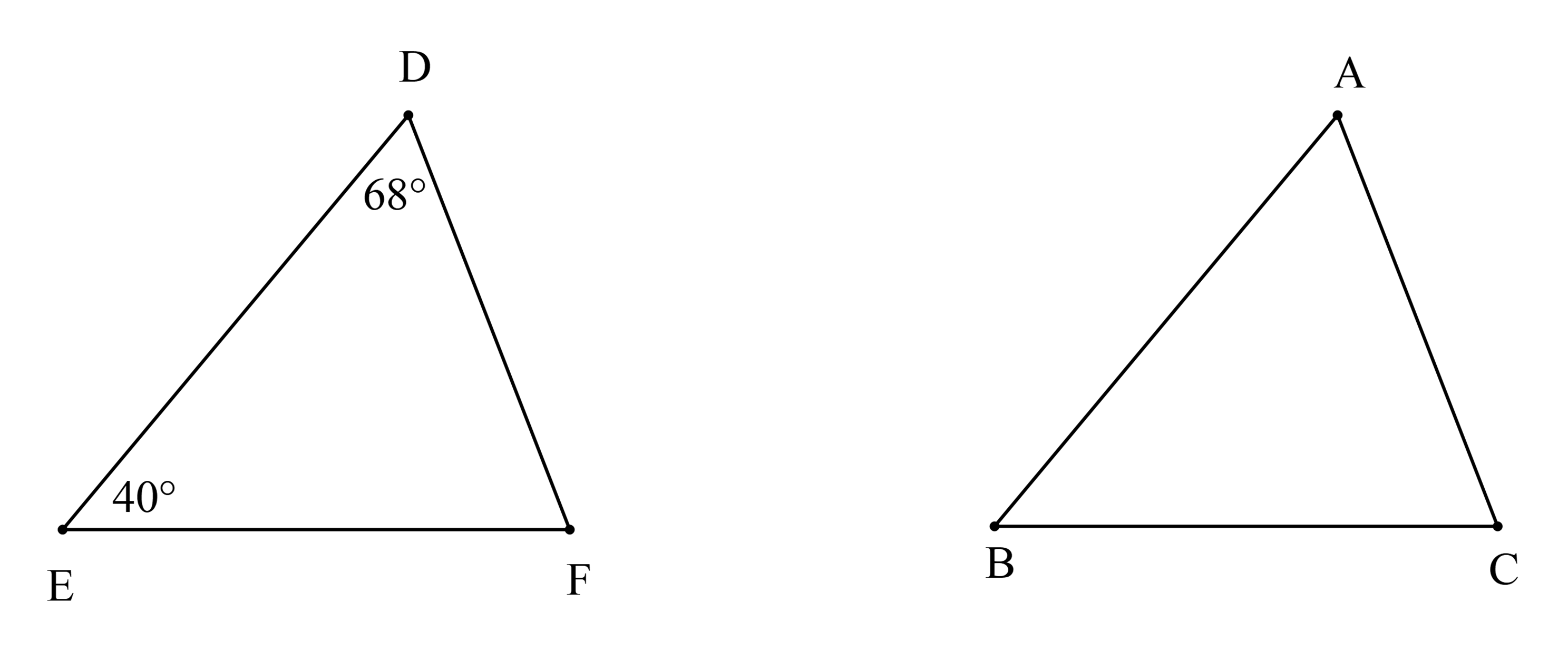
Biết ∆DEF = ∆ABC và \(\widehat {\rm{D}} = 68^\circ \); \(\widehat {\rm{E}} = 40^\circ \). Số đo của \(\widehat {\rm{C}}\) là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆DEF có \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(68^\circ + 40^\circ + \widehat {\rm{F}} = 180^\circ \)
Suy ra \(\widehat {\rm{F}} = 180^\circ - 68^\circ - 40^\circ = 72^\circ \)
Theo bài ta có ∆DEF = ∆ABC
Suy ra \(\widehat {\rm{F}} = \widehat {\rm{C}} = 72^\circ \) (hai góc tương ứng).
Vậy ta chọn phương án C.
Câu 2:
Cho hình vẽ

Biết ∆ABC = ∆MNP . Chu vi ∆MNP là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Theo bài ∆ABC = ∆MNP
Suy ra AC = MP = 9 cm (hai cạnh tương ứng)
BC = NP = 8 cm (hai cạnh tương ứng)
Chu vi ∆MNP là: MN + MP + NP = 6 + 9 + 8 = 23 (cm).
Vậy ta chọn phương án C.
Câu 3:
Cho tam giác ABC có AB = AC và AH là đường cao kẻ từ A. Biết \(\widehat B = 43^\circ ,\) số đo của \(\widehat {BAC}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
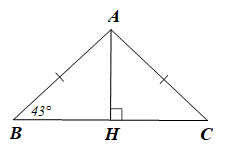
Xét ∆AHB và ∆ AHC ta có:
\(\widehat {{\rm{AHB}}} = \widehat {{\rm{AHC}}} = 90^\circ \) (giả thiết);
AH là cạnh chung;
AB = AC (giả thiết);
Suy ra ∆AHB = ∆AHC (cạnh huyền – cạnh góc vuông)
Suy ra \(\widehat {\rm{B}} = \widehat {\rm{C}} = 43^\circ \) (hai góc tương ứng)
Xét ∆ABC có: \(\widehat {{\rm{BAC}}} + \widehat {\rm{B}} + \widehat {\rm{C}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(\widehat {{\rm{BAC}}} + 43^\circ + 43^\circ = 180^\circ \)
Suy ra \(\widehat {{\rm{BAC}}} = 180^\circ - 43^\circ - 43^\circ = 94^\circ \).
Vậy ta chọn phương án D.
Câu 4:
Cho hình vẽ

Số đo của \(\widehat {AFO}\) là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆FOB và ∆EOC có:
\(\widehat {FOB} = \widehat {{\rm{EOC}}}\) (hai góc đối đỉnh);
OB = OC (giả thiết);
\(\widehat {{\rm{FBO}}} = \widehat {{\rm{ECO}}}\) (giả thiết).
Suy ra ∆FOB = ∆EOC (g.c.g)
Suy ra \(\widehat {{\rm{BFO}}} = \widehat {{\rm{CEO}}} = 88^\circ \) (hai góc tương ứng)
Ta có \(\widehat {{\rm{BFO}}} + \widehat {AFO} = 180^\circ \) (hai góc kề bù)
Hay \(88^\circ + \widehat {AFO} = 180^\circ \)
Suy ra \(\widehat {AFO} = 180^\circ - 88^\circ = 92^\circ \).
Vậy ta chọn phương án C.
Câu 5:
Cho tam giác ABC vuông tại B (AB < AC) có AM là tia phân giác góc A (M ∈ BC). Trên cạnh AC lấy điểm N sao cho AB = AN. Góc bằng với \(\widehat {{\rm{BAC}}}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B

Xét ∆ABM và ∆ANM có:
AB = AN (giả thiết),
\(\widehat {{\rm{BAM}}} = \widehat {{\rm{NAM}}}\) (do AM là tia phân giác góc A),
AM là cạnh chung.
Suy ra ∆ABM = ∆ANM (c.g.c)
Suy ra \(\widehat {{\rm{ABM}}} = \widehat {{\rm{ANM}}} = 90^\circ \) (hai góc tương ứng)
Ta có \(\widehat {{\rm{ANM}}} + \widehat {{\rm{CNM}}} = 180^\circ \) (hai góc kề bù)
Hay \(90^\circ + \widehat {{\rm{CNM}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{CNM}}} = 180^\circ - 90^\circ = 90^\circ \)
Xét ∆CNM có \(\widehat {\rm{C}} + \widehat {{\rm{CNM}}} + \widehat {{\rm{CMN}}} = 180^\circ \)(tổng ba góc trong một tam giác bằng 180°)
Hay \(\widehat {\rm{C}} + 90^\circ + \widehat {{\rm{CMN}}} = 180^\circ \)
Suy ra \(\widehat {\rm{C}} + \widehat {{\rm{CMN}}} = 180^\circ - 90^\circ = 90^\circ \) (1)
Xét ∆ABC vuông tại B có: \(\widehat {{\rm{BAC}}} + \widehat {\rm{C}} = 90^\circ \)(tổng hai góc nhọn trong tam giác vuông bằng 90°) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{BAC}}} = \widehat {{\rm{CMN}}}\).
Vậy ta chọn phương án B.
Câu 6:
Cho hình vẽ
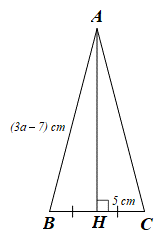
Biết rằng chu vi ∆ABC bằng 50 cm. Giá trị của a là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Xét ∆AHB và ∆ AHC ta có:
\(\widehat {{\rm{AHB}}} = \widehat {{\rm{AHC}}} = 90^\circ \) (giả thiết);
AH là cạnh chung;
BH = CH (giả thiết).
Suy ra ∆AHB = ∆AHC (c.g.c)
Suy ra AB = AC = 3a – 7 (cm) (hai cạnh tương ứng).
Ta có BC = BH + CH = 5 + 5 = 10 (cm) (vì BH = CH = 5 cm).
Do chu vi ∆ABC bằng 50 cm nên:
AB + BC + CA = 50
Hay 3a – 7 + 10 + 3a – 7 = 50
Suy ra 6a – 4 = 50
6a = 50 + 4 = 54
a = 9.
Vậy ta chọn phương án D.
Câu 7:
Cho hình vẽ

Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có \(\widehat {{\rm{ACH}}} + \widehat {{\rm{ACD}}} = 180^\circ \) (hai góc kề nhau)
Hay \(\widehat {{\rm{ACH}}} + 120^\circ = 180^\circ \)
Suy ra \(\widehat {{\rm{ACH}}} = 180^\circ - 120^\circ = 60^\circ \)
Ta có \(\frac{{\widehat {{\rm{ACD}}}}}{{\widehat {{\rm{ACH}}}}} = \frac{{120^\circ }}{{60^\circ }} = 2\) nên \(\widehat {{\rm{ACD}}} = 2\widehat {{\rm{ACH}}}\) (1)
Xét ∆AHB và ∆ AHC ta có:
\(\widehat {{\rm{AHB}}} = \widehat {{\rm{AHC}}} = 90^\circ \) (giả thiết);
AH là cạnh chung;
\(\widehat {{\rm{BAH}}} = \widehat {{\rm{CAH}}}\) (giả thiết).
Suy ra ∆AHB = ∆ AHC (cạnh góc vuông – góc nhọn kề)
Suy ra \(\widehat {\rm{B}} = \widehat {{\rm{ACH}}}\) (hai góc tương ứng) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{ACD}}} = 2\widehat {\rm{B}}\).
Vậy ta chọn phương án A.
