Cho hình thang vuông ABCD tại A và D. Gọi E, F lần lượt là trung điểm của AD
Cho hình thang vuông ABCD tại A và D. Gọi E, F lần lượt là trung điểm của AD, BC. Chứng minh:
a) ∆AFD cân tại F.
b) \(\widehat {BAF} = \widehat {CDF}\).
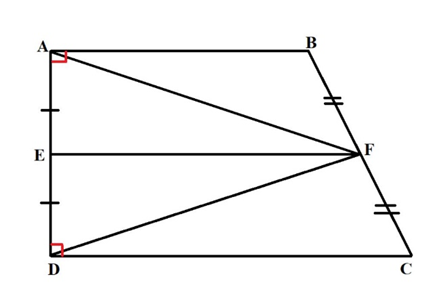
a) Ta có EF là đường trung bình của hình thang ABCD
⇒ EF // AB
Suy ra EF ⊥ AD.
Khi đó EF vừa là trung tuyến vừa là đường cao của tam giác AFD (đpcm)
Vậy tam giác AFD cân tại F.
b) Tam giác AFD cân tại F nên \(\widehat {EAF} = \widehat {EDF}\).
Suy ra \(\widehat {FAB} = \widehat {CDF}\).