Lời giải
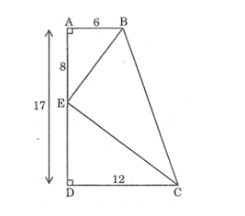
Ta có AD = AE + ED
Suy ra DE = AD – AE
Mà AE = 8 cm, AD = 17cm (giả thiết)
Nên DE = 17 – 8 = 9 (cm)
Ta có \(\frac{{{\rm{AB}}}}{{{\rm{DE}}}} = \frac{6}{9} = \frac{2}{3}\); \(\frac{{{\rm{AE}}}}{{{\rm{DC}}}} = \frac{8}{{12}} = \frac{2}{3}\)
Suy ra \(\frac{{{\rm{AB}}}}{{{\rm{DE}}}} = \frac{{{\rm{AE}}}}{{{\rm{DC}}}}\)
Xét tam giác ABE và tam giác DEC có
\(\frac{{{\rm{AB}}}}{{{\rm{DE}}}} = \frac{{{\rm{AE}}}}{{{\rm{DC}}}}\) (chứng minh trên)
\(\widehat A = \widehat D = 90^\circ \) (giả thiết)
Do đó ∆ABE đồng dạng ∆DEC (c.g.c)
Suy ra \(\widehat {ABE} = \widehat {DEC}\)
Xét tam giác ABE vuông tại A có \(\widehat {ABE} + \widehat {A{\rm{E}}B} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Mà .\(\widehat {ABE} = \widehat {DEC}\). (chứng minh trên)
Nên \(\widehat {DEC} + \widehat {A{\rm{E}}B} = 90^\circ \)
Lại có \(\widehat {DEC} + \widehat {A{\rm{E}}B} + \widehat {{\rm{CE}}B} = \widehat {A{\rm{ED}}} = 180^\circ \)
Suy ra \(\widehat {BEC} = 90^\circ \)
Vậy \(\widehat {BEC} = 90^\circ \).