Cho hình thang vuông ABCD có góc A = góc D = 90 độ

Đề bài: Cho hình thang vuông ABCD có $\widehat{\text{A}}\text{ =}\widehat{\text{ D }}{\text{= 90}}^{\text{0}}$, $\text{AB = AD = }\frac{\text{1}}{\text{2}}\text{CD}$. Gọi E là trung điểm của CD

a/ Tứ giác ABCE là hình gì?

b/ Tứ giác ABED là hình gì?

c/ Gọi M là giao điểm của AC và BE, K là giao điểm của AE và DM, O là giao điểm hai đuờng chéo hình vuông ABED. Kẻ DH vuông góc với AC cắt AE tại I. Chứng minh DB là tia phân giác của $\widehat{IDK}$

d/ Chứng minh BIDK là hình thoi

Trả lời

Hướng dẫn giải:

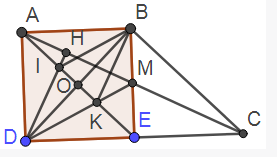
a) Xét tứ giác ABCE có AB song song và bằng EC (gt) nên nó là hình bình hành.

b) Xét tứ giác ABED có AB song song và bằng DE (gt) nên nó là hình bình hành.

Lại có $\widehat{ADE}={90}^0$  nên ABED là hình chữ nhật.

Lại có AB = AD nên ABED là hình vuông.

c) Xét tam giác AME và DMB có :

ME = B

AE = DB (Hai đường chéo hình vuông)

$\widehat{AEM}=\widehat{DBM}={45}^0$ (ABED là hình vuông)

$\Rightarrow \Delta AEM=\Delta DBM\left(c-g-c\right)\to \widehat{MAE}=\widehat{MDE}\left(1\right)$

Xét hai tam giác vuông AHI và DOI có:

$\widehat{AIH}=\widehat{DIO}$ (Hai góc đối đỉnh)

$\Rightarrow \widehat{HAI}=\widehat{DIO}$ (Cùng phụ với hai góc bên trên)    (2)

Từ (1) và (2) ta có: $\widehat{ODK}=\widehat{IDO}$ hay DO là tia phân giác của góc $\widehat{IDK}$

d)  Xét $\Delta$ IDK có DO là tia phân giác đồng thời là đường cao nên nó là tam giác cân tại D.Vậy thì DO là đường trung tuyến hay OI = OK.

Do ABED là hình vuông nên O là trung điểm BD.

Xét tứ giác DIBK có O là trung điểm hai đường chéo nên DIBK là hình bình hành.

Lại có $IK\perp DB$  nên DIBK là hình thoi.