Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD

Bài 3.11 trang 34 SBT Toán 8 Tập 1: Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C. Tính chu vi của hình thang đó biết rằng AD = 2 cm.

Trả lời

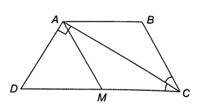
Do CA là tia phân giác của $\widehat{C}$ nên $\widehat{BCA}=\widehat{ACD}$

Mà ABCD là hình thang cân nên AB // CD, suy ra $\widehat{BCA}=\widehat{ACD}$(hai góc so le trong)

Do đó, $\widehat{BAC}=\widehat{BCA}$, suy ra ∆ABC cân tại B.

Đặt $\widehat{BAC}=\alpha$ thì $\widehat{C}=2\alpha$.

Vì ABCD là hình thang cân nên $\widehat{D}=\widehat{C}=2\alpha .$

Tam giác ADC vuông tại A nên $\widehat{ADC}+\widehat{ACD}=2\alpha +\alpha =90°,$ suy ra $\alpha =30°,\widehat{D}=60°.$

Lấy điểm M thuộc cạnh huyền DC sao cho DM = AD, mà $\widehat{D}=60°$ thì AMD là tam giác đều, nên $\widehat{MAD}=60°$

Khi đó $\widehat{MAC}=\widehat{CAD}-\widehat{MAD}=90°-60°=30°$

Suy ra $\widehat{ACM}=\widehat{CAM}=30°$ nên tam giác MAC cân tại M

Do đó AM = MC, mà AM = DM = AD

Nên AM = DM = AD = MC hay DC = 2AD.

Vậy AB = BC = AD, DC = 2AD nên chu vi hình thang bằng

AB + BC + CD + AD = 5AD = 5.2 = 10 cm.

Xem thêm các bài giải Toán lớp 8 sách Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 2

Bài 10: Tứ giác

Bài 11: Hình thang cân

Bài 12: Hình bình hành

Bài 13: Hình chữ nhật

Bài 14: Hình thoi và hình vuông