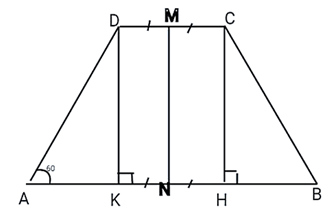
Hạ đường cao CH và DK. ⇒ DK // CH và DC // HK

⇒ DCHK là hình bình hành có \(\widehat H = 90^\circ \)

⇒ DCHK là hình chữ nhật ⇒ HK = DC = 10 cm

Xét ∆DAK = ∆CBH có:

Vì \(\widehat H = \widehat K = 90^\circ \), AD = CB ( ABCD là hình thang cân)

Và \(\widehat A = \widehat B\)( ABCD là hình thang cân)

\( \Rightarrow BH = AK = \frac{{\left( {AB - HK} \right)}}{2} = 10\) cm

Xét ∆CBH vuông tại H và có \(\widehat B = 60^\circ \)

\( \Rightarrow \widehat C = 30^\circ \Rightarrow BC = 2BH = 20\)cm

N là trung điểm AB ⇒ N là trung điểm HK

\( \Rightarrow MN = CH = \sqrt {{{20}^2} - {{10}^2}} = 10\sqrt 3 \)(cm)