Cho hình thang cân ABCD (AB // CD) có đường chéo BD chia hình thang thành hai tam giác cân: tam giác ABD cân tại A và tam giác BCD cân tại D. Tính các góc của hình thang cân đó. A. góc A = g
27
15/05/2024
Cho hình thang cân ABCD (AB // CD) có đường chéo BD chia hình thang thành hai tam giác cân: tam giác ABD cân tại A và tam giác BCD cân tại D. Tính các góc của hình thang cân đó.
A. \(\widehat A = \widehat B = 108^\circ ,\,\widehat C = \widehat D = 72^\circ \).
B. \(\widehat A = \widehat B = 120^\circ ,\,\widehat C = \widehat D = 60^\circ \).
C. \(\widehat A = \widehat B = 115^\circ ,\,\widehat C = \widehat D = 65^\circ \).
D. \(\widehat A = \widehat B = 105^\circ ,\,\widehat C = \widehat D = 75^\circ \).
Trả lời
Lời giải
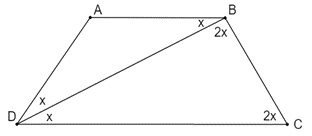
Đặt \(x = \widehat {ADB}\,\,\left( {0^\circ < x < 90^\circ } \right)\).
Ta có tam giác ADB cân tại A. Suy ra \(\widehat {ABD} = \widehat {ADB} = x\).
Lại có AB // CD (do ABCD là hình thang cân).
Suy ra \(\widehat {ABD} = \widehat {BDC} = x\) (cặp góc so le trong).
Ta có ABCD là hình thang cân. Suy ra \(\widehat {ADC} = \widehat {DCB} = 2x\).
Ta có tam giác BCD cân tại D. Suy ra \(\widehat {DBC} = \widehat {BCD} = 2x\).
Tam giác BCD cân tại D có: \(\widehat {BDC} + 2\widehat {DCB} = 180^\circ \).
Suy ra x + 2.2x = 180°.
Do đó 5x = 180°.
Vì vậy x = 36°.
Ta có \(\widehat {ADC} = \widehat {BCD} = 2x = 2.36^\circ = 72^\circ \).
Ta có \(\widehat {DAB} + \widehat {ADC} = 180^\circ \) (do AB // CD và hai góc này là hai góc so le trong).
Suy ra \(\widehat {DAB} = \widehat {ABC} = 180^\circ - \widehat {ADC} = 180^\circ - 72^\circ = 108^\circ \).
Vậy hình thang cân ABCD có các góc là: \(\widehat A = \widehat B = 108^\circ ,\,\widehat C = \widehat D = 72^\circ \).
Do đó ta chọn phương án B.

