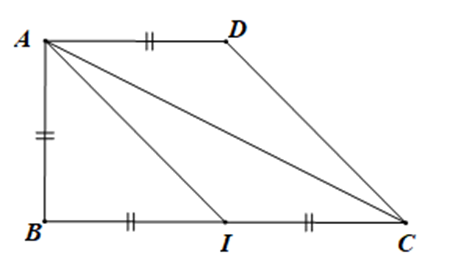
Cho hình thang ABCD vuông tại A và B, AB = AD = a, BC = 2a. Gọi I là trung điểm của BC. Tính độ dài các vectơ:
a) \[\overrightarrow a = \overrightarrow {BA} - \overrightarrow {BD} - \overrightarrow {DC} \];
b) \[\overrightarrow b = \overrightarrow {DB} - \overrightarrow {DA} + \overrightarrow {IC} \].
Ta có:
a) \[\left| {\overrightarrow a } \right| = \left| {\overrightarrow {BA} - \overrightarrow {BD} - \overrightarrow {DC} } \right|\]
\[ = \left| {\overrightarrow {DA} - \overrightarrow {DC} } \right|\]\[ = \left| {\overrightarrow {CA} } \right|\]
= CA
\[ = \sqrt {A{B^2} + B{C^2}} \]
\[ = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \]
b) \[\left| {\overrightarrow b } \right| = \left| {\overrightarrow {DB} - \overrightarrow {DA} + \overrightarrow {IC} } \right|\]
\[ = \left| {\overrightarrow {AB} + \overrightarrow {IC} } \right|\]
\[ = \left| {\overrightarrow {AB} + \overrightarrow {BI} } \right|\]\[ = \left| {\overrightarrow {AI} } \right|\]
= AI
\[ = \sqrt {A{B^2} + B{I^2}} \]
\[ = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \].