Cho hình thang ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA.

a) Tứ giác MNPQ là hình gì? Vì sao?

b) Chứng minh ABCD là hình thang cân thì MP là phân giác của góc QMN.

Lời giải

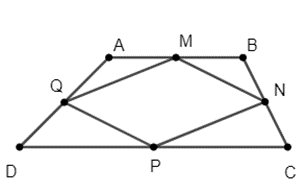
a) Xét tam giác ABC có M, N lần lượt là trung điểm của AB và BC.

Suy ra MN là đường trung bình của tam giác ABC.

Do đó MN // AC, \(MN = \frac{1}{2}AC\)   (1)

Chứng minh tương tự, ta có: QP//AC, \(QP = \frac{1}{2}AC\)    (2)

QM // BD, \(QM = \frac{1}{2}BD\)    (3)

Từ (1) và (2) suy ra tứ giác MNPQ là hình bình hành.

b) Khi ABCD là tam giác cân với AB // CD ta có AC = BD.

Từ (3) suy ra: \(QM = \frac{1}{2}BD = \frac{1}{2}AC = MN\) (4)

Theo câu a) MNPQ là hình bình hành mà mặt khác tứ giác MNPQ có QM = MN mà QM và MN là hai cạnh kề nên suy ra MNPQ là hình thoi.

Do đó MP là tia phân giác của \(\widehat {QMN}\) theo tính chất của hình thoi.