Cho hình thang ABCD có đáy lớn AD, đường chéo AC vuông góc với cạnh bên CD, góc BAC = góc CAD=. Tính AD nếu chu vi của hình thang bằng 20 cm và góc D = 60^0
19
20/05/2024
Cho hình thang ABCD có đáy lớn AD, đường chéo AC vuông góc với cạnh bên CD, \(\widehat {BAC} = \widehat {CAD}\). Tính AD nếu chu vi của hình thang bằng 20 cm và góc \(\widehat D = 60^\circ \).
Trả lời
Lời giải
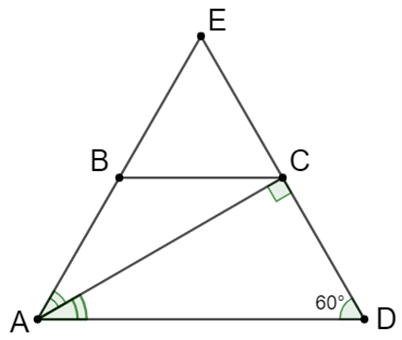
Tia AB cắt DC tại E.
Þ AC là tia phân giác của \[\widehat {DAE}\] (gt)
AC ^ CD Þ AC ^ DE.
Tam giác ADE có AC là đường cao vừa là đường phân giác nên ∆ADE là tam giác cân tại A.
Lại có: \(\widehat {ADC} = \widehat {ADE} = 60^\circ \) Þ ΔADE là tam giác đều.
Þ C là trung điểm của DE (Do AC đồng thời là trung tuyến) .
Mà: BC // AD Þ BC là đường trung bình của ΔADE.
Ta có: \(AB = DC = \frac{{AD}}{2};\;BC = \frac{{AD}}{2}\).
Giả thiết: AB + BC + CD + AD = 20
\( \Leftrightarrow \frac{{AD}}{2} + \frac{{AD}}{2} + \frac{{AD}}{2} + AD = 20\)
\( \Leftrightarrow \frac{5}{2}AD = 20 \Leftrightarrow AD = 8\).

