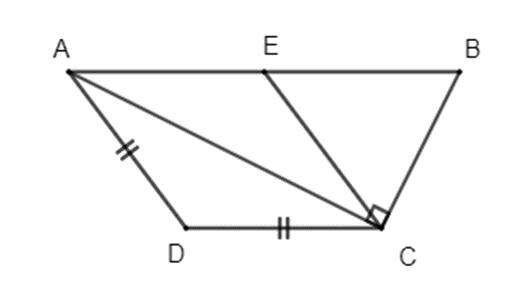
Cho hình thang ABCD (AB // CD) có AD = CD và AC vuông góc BC. Từ C kẻ đường
Cho hình thang ABCD (AB // CD) có AD = CD và AC ⊥ BC. Từ C kẻ đường thẳng song song với AD và cắt AB tại E.
a. Chứng minh tứ giác AECD là hình thoi.
b. Chứng minh tứ giác BEDC là hình bình hành.
c. Chứng minh ∆CEB cân.