Cho hình thang ABCD (AB // CD, AB < CD), hai tia phân giác của góc B
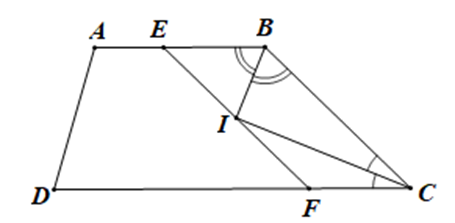
a) • Vì EF // BC nên \(\widehat {IBC} = \widehat {EIB}\) (hai góc so le trong)
Vì BI là tia phân giác của góc ABC nên \(\widehat {EBI} = \widehat {IBC} = \frac{1}{2}\widehat {ABC}\)
Suy ra \[\widehat {EBI} = \widehat {EIB}\]
Do đó tam giác BIE cân tại E.
• Vì EF // BC nên \(\widehat {BCI} = \widehat {FIC}\) (hai góc so le trong)
Vì CI là tia phân giác của góc BCD nên \(\widehat {BCI} = \widehat {FCI} = \frac{1}{2}\widehat {BCD}\)
Suy ra \(\widehat {FIC} = \widehat {FCI}\)
Do đó tam giác CIF cân tại F.
b) Vì tam giác BIE cân tại E nên BE = EI.
Vì tam giác CIF cân tại F nên FI = FC.
Ta có EF = EI + IF = BE + FC