Cho hình lập phương $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$ cạnh bằng a, $K\in C{C}^{\text{'}}$ sao cho  $CK=\frac{2}{3}a$. Mặt phẳng (α) qua $A,K$ và song song với $BD$ chia khối lập phương trình hai phần. Tính tỷ số thể tích hai phần đó.

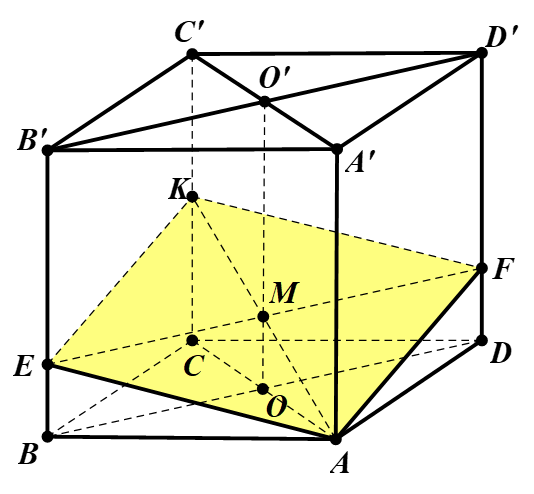
Gọi $O,O^{\text{'}}$ là tâm của hình vuông $ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}$, $M=AK\cap \text{.}$OO'
Qua M kẻ đường thẳng song song với BD cắt BB', DD' lần lượt tại E, F
Khi đó, thiết diện tạo bởi (α) và hình lập phương chính là hình bình hành AEKF.
Có OM là đường trung bình tam giác ACK nên $OM=\frac{1}{2}CK=\frac{a}{3}.$
Do đó, $BE=DF=\frac{1}{2}CK=\frac{a}{3}$. Đặt $V_1=V_{ABEKFDC},V_2=V_{AEKF{A}^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}.$
Ta có hai tứ giác bằng nhau: $BCKE=C^{\text{'}}{B}^{\text{'}}EK,$ mặt phẳng $\left(A{A}^{\text{'}}{C}^{\text{'}}C\right)$ chia khối $ABEKFDC$ thành hai phần bằng nhau nên:
$\begin{array}{l}{V}_1=2V_{A.BCKE}=2.\frac{1}{3}.AB.S_{BCKE}=\frac{2}{3}a.\frac{1}{2}.S_{BC{C}^{\text{'}}{B}^{\text{'}}}=\frac{a^3}{3}.\\ V_2=V_{ABCD.A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}{D}^{\text{'}}}-V_1=a^3-\frac{a^3}{3}=\frac{2a^3}{3}.\end{array}$
Vậy $\frac{V_1}{V_2}=\frac{1}{2}.$