Cho hình lập phương ABCD.A'B'C'D' có AC' = căn của 3. Khoảng cách giữa hai đường thẳng AB'

Bài 15 trang 106 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có AC' = $\sqrt{3}$ . Khoảng cách giữa hai đường thẳng AB' và BC' bằng

A. $\frac{1}{3}$ .

B. $\frac{\sqrt{3}}{3}$ .

C. $\frac{\sqrt{3}}{2}$ .

D. $\frac{1}{2}$ .

Trả lời

Đáp án đúng là: B

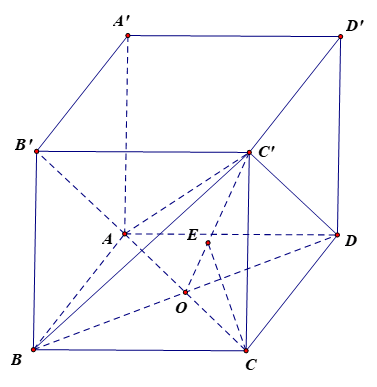
Gọi O là giao điểm của AC và BD. Vì ABCD là hình vuông nên O là trung điểm của AC, BD và AC $\perp$ BD.

Có AD // B'C' và AD = B'C' (vì cùng song song và bằng BC) nên ADC'B' là hình bình hành, suy ra AB' // DC'. Do đó AB' // (BDC').

Khi đó d(AB', BC') = d(AB', (BDC')) = d(A, (BDC')) = d(C, (BDC')) .

Giả sử hình lập phương ABCD.A'B'C'D' có cạnh là a.

Xét tam giác ABC vuông tại B có $AC=\sqrt{A{B}^2+B{C}^2}=\sqrt{a^2+a^2}=a\sqrt{2}$ .

Vì CC' $\perp$ (ABCD) nên CC' $\perp$ AC hay tam giác ACC' vuông tại C.

Xét tam giác ACC' vuông tại C, có $A{C^{\text{'}}}^2=A{C}^2+C{C^{\text{'}}}^2$$\iff 3=2a^2+a^2$$\Rightarrow a=1$ .

Do đó hình lập phương ABCD.A'B'C'D' có cạnh là 1 nên AC = $\sqrt{2}$ .

Vì O là trung điểm của AC nên CO = $\frac{\sqrt{2}}{2}$ .

Có AC $\perp$ BD, BD $\perp$ AA' (do AA' $\perp$ (ABCD)), suy ra BD $\perp$ (ACC'A') mà BD $\subset$ (BDC') nên (BDC') $\perp$ (ACC'A') .

Kẻ CE $\perp$ C'O tại E.

Vì (BDC') $\perp$ (ACC'A'), (BDC') $\cap$ (ACC'A') = C'O mà CE $\perp$ C'O nên CE $\perp$ (BDC').

Khi đó d(C, (BDC')) = CE.

Xét tam giác C'CO vuông tại C, CE là đường cao có:

$\frac{1}{C{E}^2}=\frac{1}{C{C^{\text{'}}}^2}+\frac{1}{C{O}^2}=\frac{1}{1}+\frac{1}{{\left(\frac{\sqrt{2}}{2}\right)}^2}=3$$\Rightarrow C{E}^2=\frac{1}{3}\Rightarrow CE=\frac{\sqrt{3}}{3}$.

Vậy d(AB', BC') $=\frac{\sqrt{3}}{3}$ .

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: