Cho hình chữ nhật ABCD, vẽ BH vuông góc AC tại H, tia BH cắt CD tại I và cắt đường thẳng AD tại K. Chứng minh:

a) AC . AH = BH . BK.

b) BH² = HI . HK.

Lời giải

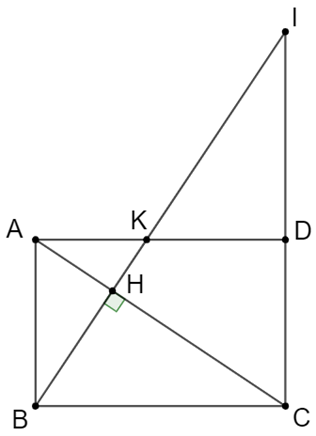
a) Áp dụng hệ thức lượng trong tam giác vuông vào ∆ABC vuông tại B có BH là đường cao.

Þ AH.AC = AB²    (1)

Áp dụng hệ thức lượng trong tam giác vuông vào ∆ABK vuông tại A có AH là đường cao.

Þ BH.BK = AB²   (2)

Từ (1) và (2) suy ra AC.AH = BH.BK (đpcm)

b) ABCD là hình chữ nhật suy ra AB // CD hay AB // CI.

Áp dụng định lí Ta lét, ta có: \(\frac{{AH}}{{HC}} = \frac{{BH}}{{HI}}\)       (3)

ABCD là hình chữ nhật suy ra AD // BC hay AK // BC.

Áp dụng định lí Ta lét, ta có: \(\frac{{AH}}{{HC}} = \frac{{KH}}{{HB}}\)     (4)

Từ (3) và (4) suy ra \(\frac{{BH}}{{HI}} = \frac{{KH}}{{HB}} \Rightarrow B{H^2} = HI\,.\,HK\) (đpcm).