Cho hình chữ nhật ABCD, M là điểm bất kì nằm trong hình chữ nhật. Chứng minh rằng

Đề bài: Cho hình chữ nhật ABCD, M là điểm bất kì nằm trong hình chữ nhật. Chứng minh rằng: MA² + MC² = MB² + MD².

Trả lời

Hướng dẫn giải:

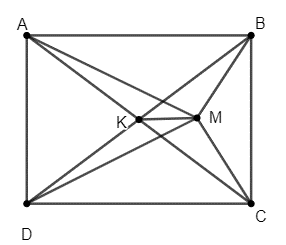
Gọi K là giao điểm của hai đường chéo AC và BD suy ra K là trung điểm của AC và BD.

Trong $\Delta MAC$  có:

$M{A}^2+M{C}^2=2M{K}^2+\frac{1}{2}A{C}^2$ (1) (công thức trung tuyến).

Trong $\Delta MBD$ : $M{B}^2+M{D}^2=2M{K}^2+\frac{1}{2}B{D}^2$  (2) (công thức trung tuyến)

Mặt khác AC = BD (3) (đường chéo hình chữ nhật)

Từ (1) và (2), (3) suy ra MA² + MC² = MB² + MD² (đpcm).