Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N lần lượt là hình chiếu của O trên AB, BC

Luyện tập 1 trang 110 Toán 8 Tập 1: Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N lần lượt là hình chiếu của O trên AB, BC. Chứng minh $MN=\frac{1}{2}AC$.

Trả lời

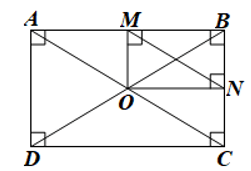
Do M, N lần lượt là hình chiếu của O trên AB, BC nên OM ⊥ AB và ON ⊥ BC.

Xét tứ giác OMBN có $\widehat{OMB}=\widehat{MBN}=\widehat{BNO}=90°$.

Do đó tứ giác OMBN là hình chữ nhật.

Suy ra OB = MN.

Do ABCD là hình chữ nhật nên OB = OD = $MN=\frac{1}{2}AC$

Khi đó $MN=OB=\frac{1}{2}AC$.

Vậy $MN=\frac{1}{2}AC$.

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

Bài 3: Hình thang cân

Bài 4: Hình bình hành