Cho hình chữ nhật ABCD có (AD < AB). Qua C kẻ đường thẳng vuông góc với đường chéo AC tại C, cắt đường thẳng AD, AB lần lượt tại M, N.

a) Chứng minh rằng AB.AN = AD.AM.

b) Cho AD = 3 cm, AB = 4 cm. Tính DM và S_AMN.

c) Chứng minh CD.CB = AB.AD.

d) Gọi E là trung điểm của MC, kẻ CH vuông DB tại H. Cho EB cắt CH tại K. Chứng minh K là trung điểm của CH.

Lời giải

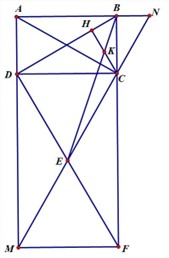
a) Xét ∆ACN vuông tại C có CB ^ AN.

Þ AC² = AB.AN (Hệ thức lượng trong tam giác vuông)

Tương tự AC² = AD.AM

Þ AB.AN = AD.AM

b) Ta có ABCD là hình chữ nhật Þ CD = AB = 4

Xét ∆ACM vuông tại C, CD ^ AM

Þ CD² = DA.DM

\( \Rightarrow DM = \frac{{C{D^2}}}{{AD}} = \frac{{16}}{3}\)

\( \Rightarrow AM = AD + DM = \frac{{25}}{3}\)

Mà \(AC = \sqrt {A{B^2} + A{D^2}} = 5\)

AC² = AB.AN \( \Rightarrow AN = \frac{{A{C^2}}}{{AB}} = \frac{{25}}{4}\)

\( \Rightarrow {S_{AMN}} = \frac{1}{2}AM.AN = \frac{{625}}{{24}}\)

c) Ta có: CD.CB = AB.AD = 12.

d) Gọi BC Ç DE = F.

Ta có E là trng điểm CM, ∆DCM vuông tại D

\[ \Rightarrow \widehat {EDC} = \widehat {ECD} = \widehat {MCD} = {90^ \circ } - \widehat {ACD} = \widehat {DAC} = \widehat {ADB}\]

\( \Rightarrow \widehat {FDB} = \widehat {FDC} + \widehat {CDB} = \widehat {ADB} + \widehat {CDB} = \widehat {ADC} = 90^\circ \)

Þ FD ^ BD Þ DF // CH

Ta có: CF // DM \( \Rightarrow \frac{{ED}}{{EF}} = \frac{{EM}}{{EC}} = 1\)

Þ ED = EF Þ E là trung điểm DF

Mà CH // DF

\( \Rightarrow \frac{{HK}}{{DE}} = \frac{{BK}}{{BE}} = \frac{{CK}}{{EF}}\)

Þ KH = KC.

Vậy K là trung điểm của CH.