Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh bằng 2, $SA=2$ và SA vuông góc với mặt phẳng đáy $\left(ABCD\right)$. Gọi $M,N$ là hai điểm thay đổi trên hai cạnh $AB,AD$ sao cho mặt phẳng $\left(SMC\right)$ vuông góc với mặt phẳng $\left(SNC\right)$. Tính tổng $T=\frac{1}{A{M}^2}+\frac{1}{A{N}^2}$ khi thể tích khối chóp $S.AMCN$ đạt giá trị lớn nhất.

Chọn C

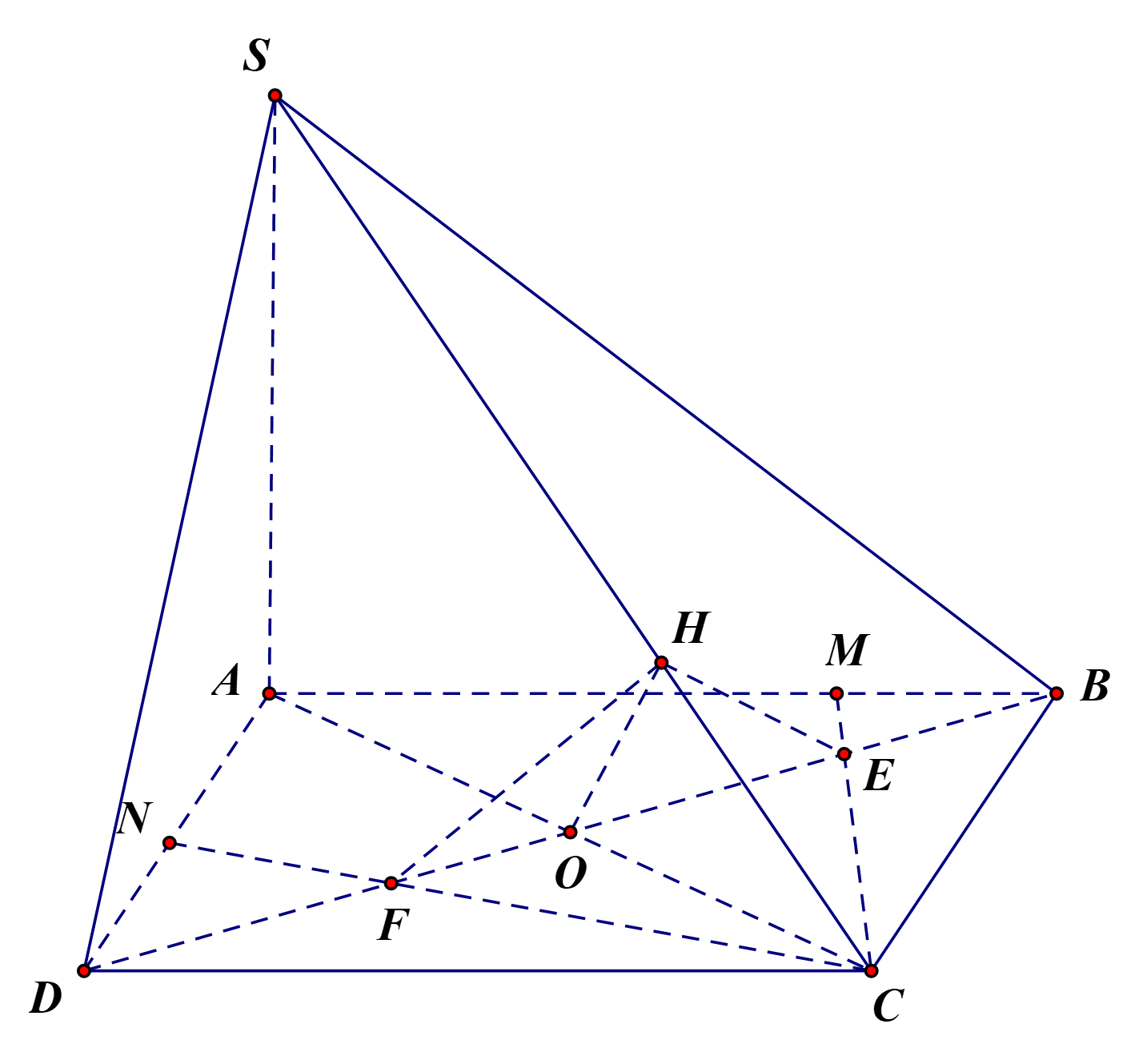
Gọi $E,F$ lần lượt là giao điểm của BD với CM và CN. Gọi O là tâm  hình vuông $ABCD$.
Theo giả thiết, ta có $BD\perp \left(SAC\right)$
Gọi H là hình chiếu của O lên BC
$\Rightarrow SC\perp \left(HEF\right)$
Vì $\left(SMC\right)\perp \left(SNC\right)$ nên $HE\perp HF$
$\Rightarrow \Delta HEF$ vuông tại H có chiều cao OH.
$\Rightarrow OE.OF=O{H}^2$
Trong đó: $OH=OC.\sin \widehat{SCA}=OC.\frac{SA}{SC}=\frac{2}{\sqrt{6}}$$\Rightarrow OE.OF=\frac{2^2}{6}=\frac{2}{3}$ (1).
Đặt $AM=x,(x>0)$, $AN=y,(y>0)$.
Xét $\Delta ABC$, gọi K là trung điểm của AM.

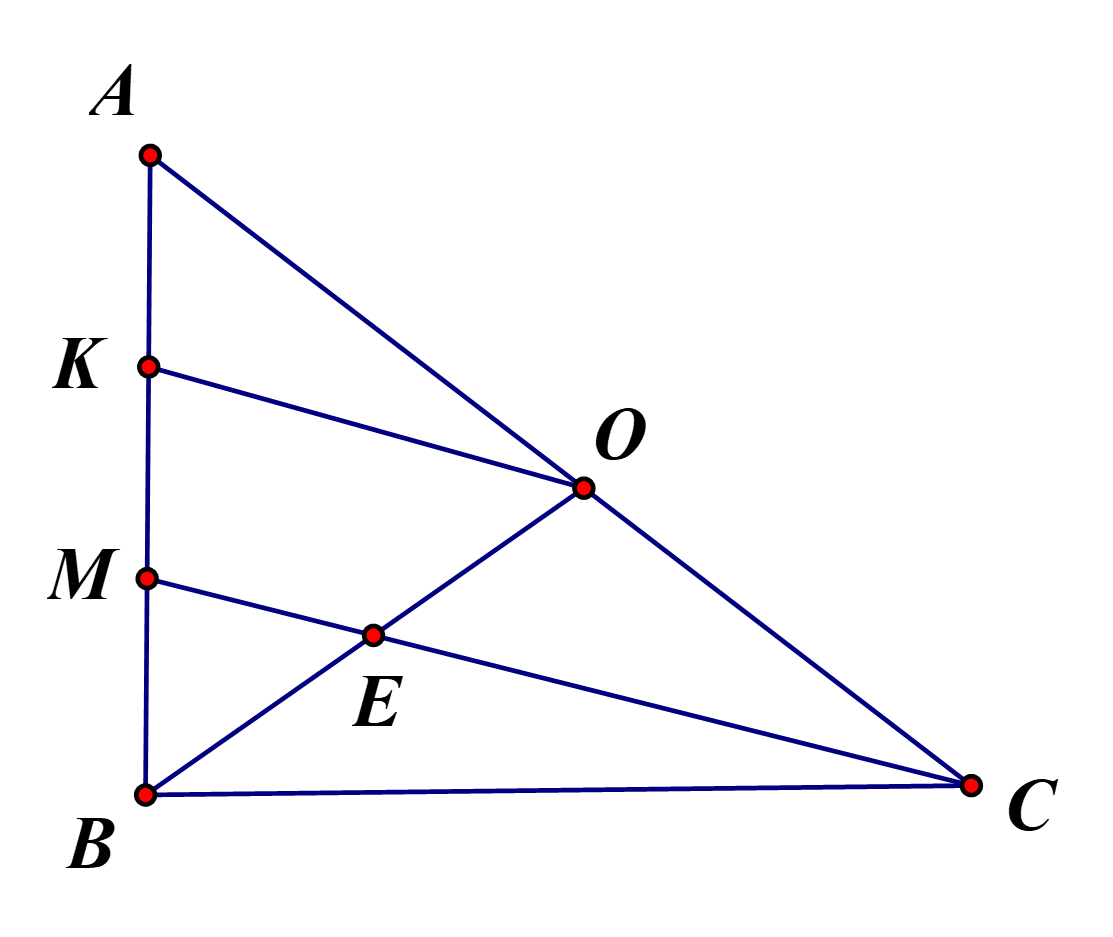
Khi đó: $OK\text{//}CM$ $\Rightarrow \frac{BE}{OE}=\frac{BM}{MK}$ $\Rightarrow \frac{OB-OE}{OE}=\frac{2-x}{\frac{x}{2}}=\frac{2\left(2-x\right)}{x}$

Chứng minh tương tự, ta có: $OF=\frac{2y\sqrt{2}}{2\left(4-y\right)}$
Từ (1) suy ra $\frac{4xy}{2\left(4-x\right)\left(4-y\right)}=\frac{2}{3}$ $\iff 3xy=\left(4-x\right)\left(4-y\right)\iff \left(x+2\right)\left(y+2\right)=12$(2) 
Ta lại có: $S_{AMCN}=S_{AMC}+S_{ANC}=\frac{1}{2}AC.AM.\sin {45}^o+\frac{1}{2}AC.AM.\sin {45}^o=\left(x+y\right)$
$\Rightarrow V_{S.AMCN}=\frac{1}{3}SA.\left(x+y\right)=\frac{2}{3}\left(x+y\right)$
Từ (2) suy ra $V_{S.AMCN}=\frac{2}{3}\left(x-2+\frac{12}{x+2}\right)$
Từ (2) suy ra $y=\frac{12}{x+2}-2$
Vì N thuộc cạnh AD nên $y\le 2\Rightarrow \frac{12}{x+2}-2\le 2\iff x\ge 1$$\Rightarrow x,y\in \left[1;2\right]$
Xét hàm số: $f\left(x\right)=\frac{2}{3}\left(x-2+\frac{12}{x+2}\right)$, với $x\in \left[1;2\right]$
Ta có: $f^{\text{'}}\left(x\right)=\frac{2}{3}\left(1-\frac{12}{{\left(x+2\right)}^2}\right)=\frac{2}{3}.\frac{x^2+4x-8}{{\left(x+2\right)}^2}$
$f^{\text{'}}\left(x\right)=0\iff x^2+4x-8=0\iff x=2\left(\sqrt{3}-1\right)$
Ta lại có:$f\left(1\right)=f\left(2\right)=2$ , $f\left(2(\sqrt{3}-1)\right)=\frac{8\left(\sqrt{3}-1\right)}{3}$.
Giá trị lớn nhất của $V_{S.AMCN}=2$ khi $x=1,y=2$ hoặc $x=2,y=1$ .
$\Rightarrow T=\frac{1}{A{M}^2}+\frac{1}{A{N}^2}=\frac{4}{2^2}+\frac{1}{2^2}=\frac{5}{4}$