Cho hình chóp tứ giác đều S.ABCD đáy là hình vuông cạnh a, cạnh bên hớp với đáy một góc ${60}^{°}$. Gọi M là trung điểm của SC. Mặt phẳng qua  A,M  và song song với BD cắt SB, SD lần lượt tại E và F và chia khối chóp S.ABCD  là hai phần, khối chóp S.AEMF và đa diện $AEMFBCD$. Tính thể tích của khối đa diện $AEMFBCD$?

Chọn B

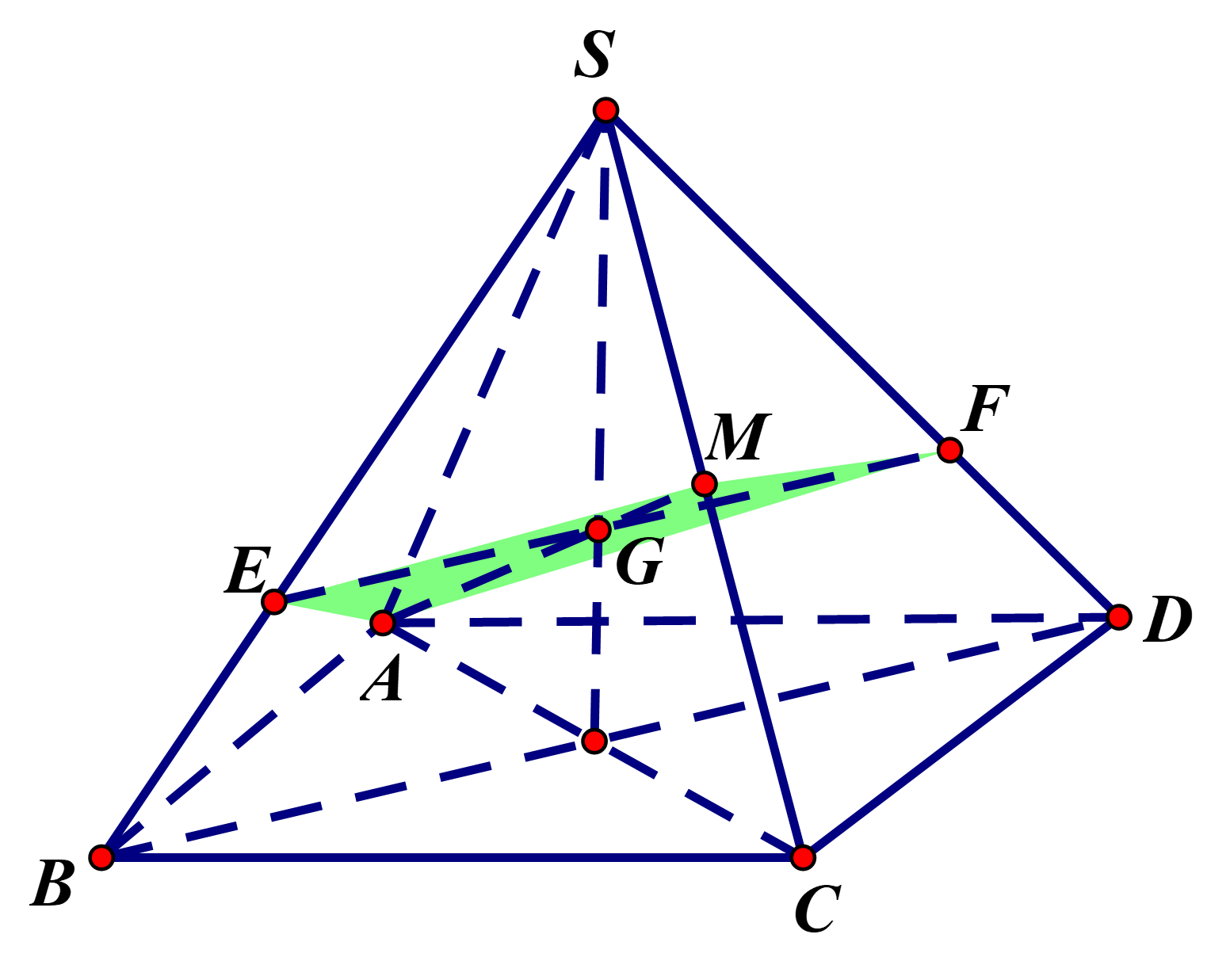
ABCD là hình vuông cạnh a, tâm O, nên $AO=\frac{a\sqrt{2}}{2}$
Xét tam giác $\Delta SAO$ vuông tại O và $\widehat{SAO}={60}^{°}$,
nên $\tan \widehat{SAO}=\frac{SO}{AO}\Rightarrow SO=\frac{a\sqrt{2}}{2}\sqrt{3}=\frac{a\sqrt{6}}{2}$
Ta có, thể tích khối chóp $S.ABCD$ là: $V=\frac{1}{3}SO.S_{ABCD}=\frac{1}{3}\frac{a\sqrt{6}}{2}.a^2=\frac{a^3\sqrt{6}}{6}\left(dvtt\right)$
Gọi G là giao điểm của AM và SO. Vì AM và SO là 2 trung tuyến của tam giác đó, nên G  là trọng tâm của nó. Ta có $SG=\frac{2}{3}SO$
Mặt phẳng A, M  qua và song song với BD đi qua G và cắt SB, SD lần lượt tại E và F ta suy ra $EF//BD$. Thiết diện tạo bởi mặt phẳng đó với hình chóp là tứ giác$AEMF,$ chia khối chóp thành 2 phần: Khối chóp $S.AEMF$ và phần còn lại, đa diện $AEMFBCD$
Xét tam giác SBD, vì EF song song với BD nên ta có $\frac{SE}{SB}=\frac{SF}{SD}=\frac{SG}{SO}=\frac{2}{3}$, nên ta có:
$\frac{V_{S.AEM}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SE}{SB}.\frac{SM}{SC}=\frac{1}{3}$. Vì $V_{S.AEMF}=2V_{S.AEM},V_{S.ABC}=\frac{1}{2}{V}_{S.ABCD}$, nên
$\begin{array}{l}{V}_{S.AEMF}=2.V_{S.AEM}=2.\frac{1}{3}{V}_{S.ABCD}=\frac{a^3\sqrt{6}}{18}\left(dvtt\right)\\ \Rightarrow V_{AEMFBCD}=\frac{a^3\sqrt{6}}{6}-\frac{a^3\sqrt{6}}{18}=\frac{a^3\sqrt{6}}{9}\left(dvtt\right)\end{array}$