Cho hình chóp tứ giác đều S.ABCD có mặt bên (SCD) hợp với mặt đáy một góc 45 độ
Cho hình chóp tứ giác đều S.ABCD có mặt bên (SCD) hợp với mặt đáy một góc và khoảng cách từ điểm A đến mặt phẳng (SCD) bằng . Tính thể tích của khối chóp .
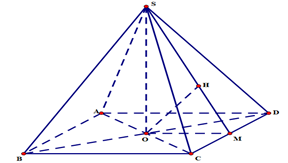
Gọi M là trung điểm cạnh CD,
Ta có tại M trong
và tại trong (ABCD).
Khi đó: . Suy ra: vuông cân tại O
Ta có tại M trong
và tại trong (ABCD).
Khi đó: . Suy ra: vuông cân tại O
Trong (SOM), dựng tại H. Mặt khác (do ) suy ra tại H.
Ta có
Theo gt:
Áp dụng hệ thức lượng trong tam giac vuông SOM:
(vì )
Suy ra: .
KL: