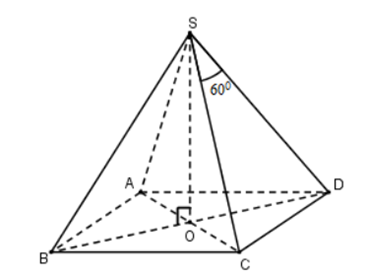
Gọi O = AC ∩ BD

Vì chóp S.ABCD đều nên SO ⊥ (ABCD)

Đặt SA = SB = SC = SD = a

∆SCD có: SC = SD; \(\widehat {CSD} = 60^\circ \Rightarrow \Delta SCD\)đều ⇒ CD = SC = SD = a

⇒ Hình vuông cạnh ABCD cạnh a ⇒ AC = BD = \(a\sqrt 2 \Rightarrow OC = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)

SO ⊥ (ABCD) ⇒ SO ⊥ OC ⇒ ∆SOC vuông tại O

\( \Rightarrow SO = \sqrt {S{C^2} - O{C^2}} \Rightarrow h = \sqrt {{a^2} - \frac{{{a^2}}}{2}} = \frac{{a\sqrt 2 }}{2} \Rightarrow a = h\sqrt 2 \)

\( \Rightarrow {S_{ABCD}} = {a^2} = {(h\sqrt 2 )^2} = 2{h^2}\)

Vậy \({V_{S.ABCD}} = \frac{1}{3}SO.{S_{ABCD}} = \frac{1}{3}h.2{h^2} = \frac{{2{h^3}}}{3}\).