Cho hình chóp tam giác S.ABC có SA vuông góc với mặt đáy, tam giác ABC cân tại A. Trên cạnh AB lấy điểm D sao cho AB=3AD. Gọi H là hình chiếu của B trên CD, M là trung điểm đoạn thẳng CH. Tính theo a  thể tích khối chóp $S.ABM$ biết $SA=AM=a$ và $BM=\frac{2}{3}a$.

Chọn C

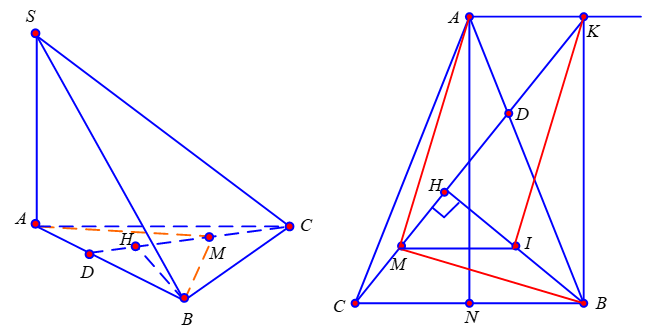
Trong mặt phẳng đáy $\left(ABC\right)$ : Kẻ $Ax\text{\hspace{0.33em}//\hspace{0.33em}}BC$ và $Ax\cap CD=K$, gọi N là trung điểm của BC. Khi đó do $\Delta ABC$ cân ở A nên $AN\perp BC$ và tứ giác $ANBK$ là hình chữ nhật.
Suy ra $CN=BN=AK$;$KB\perp BC$
Gọi I là trung điểm của BH, do M là trung điểm đoạn thẳng CH nên $MI\text{//}BC$ và $MI=\frac{1}{2}BC$ (đường trung bình của tam giác $\Delta BHC$. Vậy $MI\text{\hspace{0.33em}//\hspace{0.33em}}AK$, $MI\perp BK$ và $MI=AK$ hay tứ giác $AMIK$ là hình bình hành và I là trực tâm của tam giác $BMK$.
Suy ra $IK\perp BM$ và $AM\text{//}IK$ nên $AM\perp BM$.
Vậy $\Delta AMB$ vuông tại M. Suy ra $S_{\Delta ABM}=\frac{1}{2}AM.BM$
Theo giả thiết ta có: $V_{S.ABM}=\frac{1}{3}SA.S_{\Delta ABM}=\frac{1}{6}SA.AM.BM$ ; với $SA=AM=a$ và $BM=\frac{2}{3}a$. Suy ra $V_{S.ABM}=\frac{1}{3}SA.S_{\Delta ABM}=\frac{1}{6}SA.AM.BM$
.