Đề bài: Cho hình chóp S.ABCD, đáy là hình thang có đáy lớn là AB. Gọi M, N lần lượt là trung điểm của SA, SB.
a) Chứng minh MN // CD.
b) Tìm giao điểm P của SC và (AND).
c) Gọi I là giao điểm của AN và DP. Chứng minh SI // AB // CD.
Hướng dẫn giải:
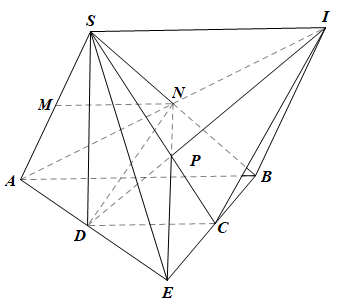
a) Xét tam giác SAB có M là trung điểm của SA, N là trung điểm của SB
Suy ra MN là đường trung bình của tam giác
Do đó MN // AB (tính chất đường trung bình của tam giác)
Mà AB // CD (do ABCD là hình thang).
Suy ra MN // CD.
b) Trong mp(ABCD), gọi E là giao điểm của BC và AD.
Khi đó E ∈ AD ⊂ (AND) nên mp(AND) chính là mp(ANE);
E ∈ BC ⊂ (SBC) nên mp(SBC) chính là mp(SBE).
Trong mp(SBE), gọi P là giao điểm của EN và SC.
Ta có: (ANE) ∩ (SBE) = NE;
NE ∩ SC = P
Suy ra SC ∩ (ANE) = P.
Do đó P là giao điểm của SC và (AND).
c) Do AN ∩ DP = {I} nên ta có:
• I ∈ DP, DP ⊂ (SCD) do đó I ∈ (SCD).
• I ∈ AN, AN ⊂ (SAB) do đó I ∈ (SAB).
Ta có: S ∈ (SAB) và S ∈ (SCD) nên (SAB) ∩ (SCD) = S;
I ∈ (SAB) và I ∈ (SCD) nên (SAB) ∩ (SCD) = I.
Do đó (SAB) ∩ (SCD) = SI.
Lại có AB // CD; AB ⊂ (SAB) và CD ⊂ (SCD)
Suy ra SI // AB // CD.