Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm tam giác SAB

Câu 14: Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm tam giác SAB, SAD. Gọi M là trung điểm của CD. Tìm giao điểm E của SD và mặt phẳng IJM.

Trả lời

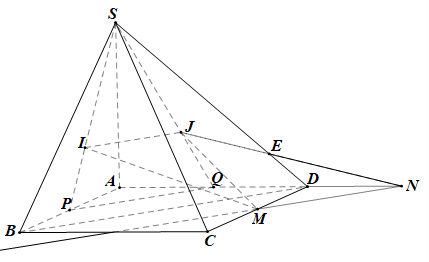
Gọi P, Q lần lượt là trung điểm của AB, AD.

Khi đó PQ là đường trung bình của tam giác ABD nên PQ // BD.

Do I, J lần lượt là trọng tâm tam giác SAB, SAD nên $\frac{SI}{SP}=\frac{2}{3}=\frac{SJ}{SQ}$ .

Do đó IJ // PQ, suy ra IJ // BD

Có IJ // BD, IJ ⊂ (IJM), BD ⊂ (ABCD)

⇔ giao tuyến của (IJM) và (ABCD) là đường thẳng qua M và song song với BD.

Đường thẳng này cắt AD tại N.

Khi đó mp(IJM) chính là mp (IJNM), mp(SAD) chính là mp(SAN)

Trong mp(SAN), JN cắt SD tại E.

Ta có: JN ∩ SD = {E}; JN ⊂ (IJM)

Khi đó E là giao điểm của SD và (IJM).