Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm
127
08/05/2023
Đề bài: Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M,N lần lượt là trung điểm các cạnh SA và SD. 1. Chứng minh MO song song với mặt phẳng (SBC) và mặt phẳng (OMN) song song với mặt phẳng (SBC).
2. Gọi K là trung điểm của MO. Chứng minh NK song song với (SBC).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (OMN). Hỏi thiết diện là hình gì ?
Trả lời
Hướng dẫn giải:
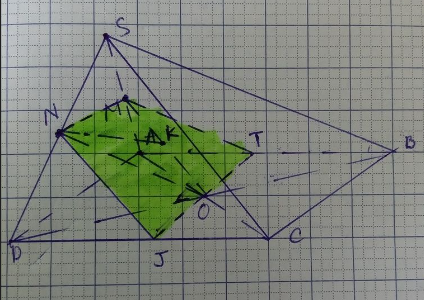
1) Ta có: MO là đường trung bình ΔSAC nên MO//SC mà SC⊂(SBC)
Vậy MO//(SBC)
Ta có:
MO//SC
NO//SB
MO, NO⊂(OMN); SC, SB⊂(SBC)
Vậy (OMN)//(SBC)
2) Ta có: (OMN)//(SBC)
Mà NK ⊂ (OMN)
Nên NK//(SBC)
3) Xét (OMN) và (ABCD):
Ta Có:
+) O là điểm chung 1
+) NM//AD (đường TB của tam giác)
Qua O vẽ đường thẳng song song với AD cắt AB tại T, cắt CD tại J
Vậy JT =(OMN) ∩ (ABCD) (1)
(OMN) ∩ (SAD)=MN (2)
(OMN) ∩ (SCD)=NJ (3)
(OMN) ∩ (SAB)=MT (4)
Từ 4 điều trên vậy thiết diện hình thang NMTJ (vì NM//TJ//AD).

